Divide 6 13 By 6 12
listenit
May 25, 2025 · 5 min read
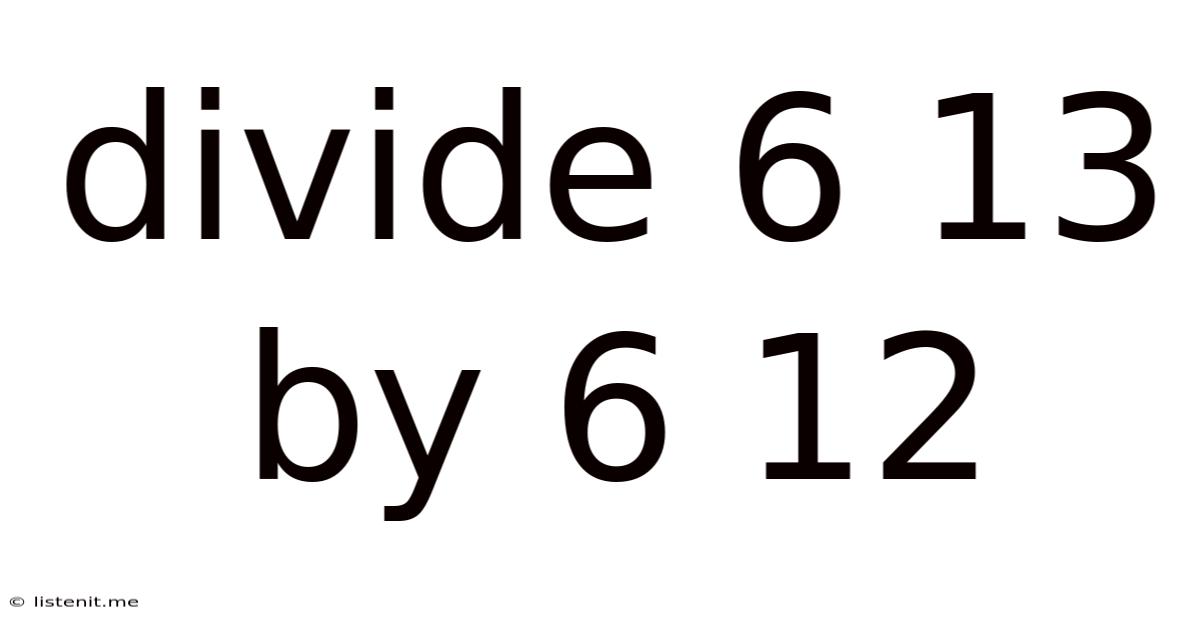
Table of Contents
Dividing 6/13 by 6/12: A Deep Dive into Fraction Division
This article will comprehensively explore the process of dividing the fraction 6/13 by the fraction 6/12. We'll go beyond simply providing the answer, delving into the underlying mathematical principles, providing multiple approaches to solve the problem, and examining the broader context of fraction division. This in-depth analysis will benefit students, educators, and anyone seeking a robust understanding of this fundamental mathematical concept.
Understanding Fraction Division
Before diving into the specific problem, let's establish a solid foundation in understanding how to divide fractions. The core concept revolves around the reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
The Key Rule: To divide one fraction by another, you multiply the first fraction by the reciprocal of the second fraction.
This rule simplifies the process considerably, transforming a division problem into a multiplication problem, which is generally easier to handle.
Method 1: Using the Reciprocal
Let's apply this rule to our problem: 6/13 ÷ 6/12.
-
Identify the reciprocal: The reciprocal of 6/12 is 12/6.
-
Rewrite as multiplication: The division problem now becomes: 6/13 × 12/6
-
Simplify before multiplying: Notice that we can simplify before multiplying. Both the numerator of the first fraction (6) and the denominator of the second fraction (6) share a common factor of 6. We can cancel these out:
(6/13) × (12/6) = (1/13) × (12/1)
-
Multiply the numerators and denominators: Multiplying the numerators (1 x 12 = 12) and the denominators (13 x 1 = 13), we get 12/13.
Therefore, 6/13 ÷ 6/12 = 12/13.
Method 2: Converting to Improper Fractions (for more complex scenarios)
While the previous method is efficient for this specific problem, let's consider a slightly different approach using improper fractions, which is beneficial when dealing with more complex fractions involving mixed numbers. Although not strictly necessary here, it's a valuable technique to master.
This method involves two steps:
-
Convert Mixed Numbers (if any): Our fractions are already in proper fraction form, so this step is skipped.
-
Multiply by the reciprocal: This step remains the same as in Method 1. We'd still multiply 6/13 by the reciprocal of 6/12 (which is 12/6). The simplification and final multiplication would yield the same result: 12/13.
Method 3: Using Decimal Equivalents (for approximation)
While not always precise, converting fractions to decimals can provide a quick approximation. This is particularly useful for estimation purposes or when working with calculators.
-
Convert to decimals: 6/13 ≈ 0.4615 and 6/12 = 0.5
-
Perform decimal division: 0.4615 ÷ 0.5 ≈ 0.923
-
Convert back to a fraction (optional): Converting 0.923 back to a fraction is more complex and will not yield the exact result as the fractional methods.
Why Method 1 is Preferred for this Problem
For the specific problem of 6/13 ÷ 6/12, Method 1 (using the reciprocal and simplifying before multiplication) is the most efficient and straightforward approach. It avoids unnecessary conversions and allows for easy simplification, leading to a clear and concise solution.
Exploring the Concepts Further: Understanding the "Why"
The process of dividing fractions might seem arbitrary at first, but it's rooted in sound mathematical principles. Consider this analogy:
Imagine you have 6/13 of a pizza, and you want to divide that share into portions of 6/12 (or 1/2) of a pizza. How many 1/2 pizza portions fit into your 6/13 portion?
This translates directly to the division problem: 6/13 ÷ 6/12. The solution, 12/13, means that roughly 12 out of 13 halves of a pizza would fit into your 6/13 share. This illustrates that dividing by a fraction is essentially asking "how many times does this fraction fit into the other?"
Advanced Applications and Problem Solving Strategies
The principles of fraction division extend far beyond simple numerical problems. They are crucial in many areas, including:
-
Algebra: Solving algebraic equations often involves manipulating fractions and applying division principles.
-
Calculus: Derivatives and integrals frequently involve manipulating fractional expressions and applying division rules.
-
Physics and Engineering: Many physical quantities and engineering calculations are expressed as fractions and require division operations for problem-solving.
-
Everyday Life: Dividing recipes, calculating proportions for construction projects, and sharing resources fairly often involve working with fractions and the principles of division.
Troubleshooting Common Errors
Several common mistakes can occur when dividing fractions. Here are some to watch out for:
-
Forgetting the reciprocal: The most frequent error is failing to take the reciprocal of the second fraction before multiplying. Remember: you multiply by the reciprocal, not directly by the second fraction.
-
Incorrect simplification: Improper or incomplete simplification can lead to inaccurate results. Always look for common factors between numerators and denominators before multiplying.
-
Mixed number errors: When working with mixed numbers, be careful to convert them to improper fractions correctly before performing the division.
-
Decimal approximation issues: Remember that using decimal approximations can introduce rounding errors, making the final result less accurate than the fractional approach.
Conclusion
Dividing fractions, specifically solving 6/13 ÷ 6/12, involves a straightforward yet fundamental mathematical concept. Mastering this process is crucial for success in various mathematical fields and practical applications. By understanding the underlying principles and practicing different solution methods, you can confidently tackle fraction division problems and build a stronger mathematical foundation. The key takeaway is to always remember the crucial step of using the reciprocal of the second fraction before proceeding with multiplication and simplification. Through diligent practice and careful attention to detail, you will become proficient in this essential mathematical skill. Remember to always check your work for simplification opportunities to ensure accuracy and efficiency.
Latest Posts
Latest Posts
-
December 25 2023 Day Of The Week
May 25, 2025
-
What Is 50 Percent Of 70
May 25, 2025
-
98 Divided By 13 With Remainder
May 25, 2025
-
What Year Was It 48 Years Ago
May 25, 2025
-
5 Out Of 40 As A Percentage
May 25, 2025
Related Post
Thank you for visiting our website which covers about Divide 6 13 By 6 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.