What Is 50 Percent Of 70
listenit
May 25, 2025 · 5 min read
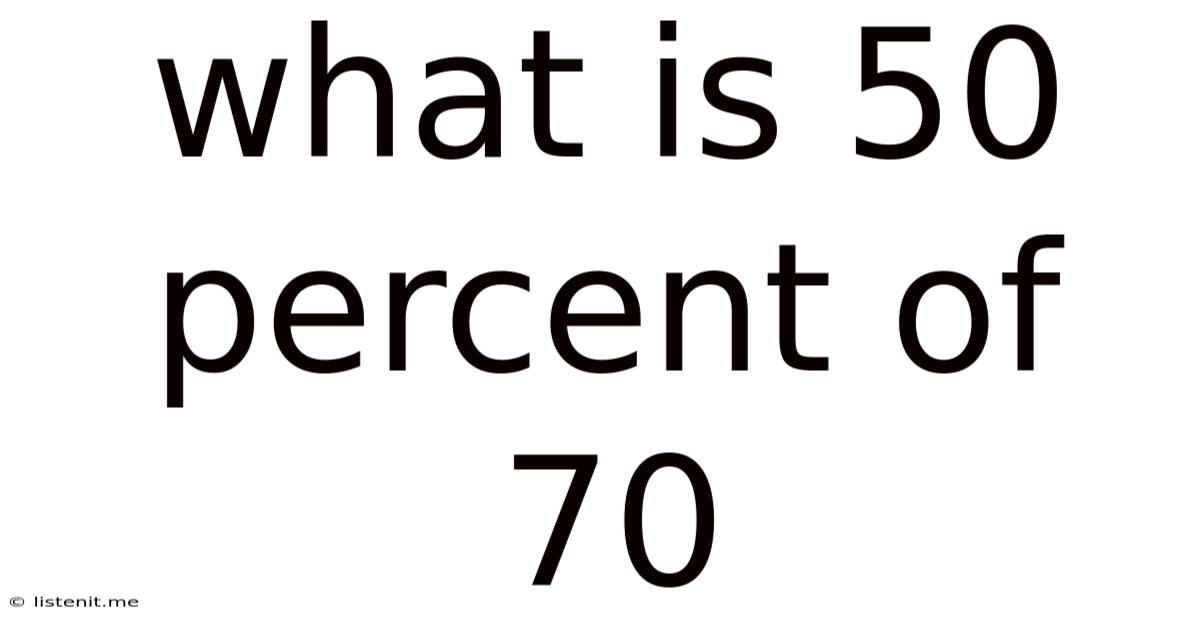
Table of Contents
What is 50 Percent of 70? A Deep Dive into Percentages and Their Applications
Finding 50 percent of 70 might seem like a simple arithmetic problem, easily solvable with a quick calculation. However, understanding the underlying concepts of percentages and their widespread applications is crucial for navigating various aspects of life, from finance and shopping to data analysis and scientific research. This article will not only answer the question "What is 50 percent of 70?" but will also explore the broader context of percentages, providing you with a comprehensive understanding of this fundamental mathematical concept.
Understanding Percentages: A Foundation for Calculation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin words "per centum," meaning "out of one hundred." This means that 50 percent represents 50 parts out of a total of 100 parts, or 50/100, which simplifies to 1/2 or 0.5. This fundamental understanding is critical for solving percentage problems.
Key Concepts:
-
TheWhole: This represents the total amount or quantity you're working with. In our example, 70 is the whole.
-
The Percentage: This is the portion of the whole you're interested in. In our case, it's 50%.
-
The Part: This is the result of calculating the percentage of the whole. This is what we are looking for.
Calculating 50 Percent of 70: Methods and Approaches
There are several ways to calculate 50 percent of 70. Let's explore the most common methods:
Method 1: Using the Fraction Equivalent
Since 50 percent is equivalent to 1/2, finding 50 percent of 70 is the same as finding half of 70. This is a straightforward calculation:
70 / 2 = 35
Therefore, 50 percent of 70 is 35.
Method 2: Using Decimal Conversion
We can convert the percentage to a decimal by dividing it by 100:
50% / 100 = 0.5
Then, multiply this decimal by the whole number:
0.5 * 70 = 35
This method demonstrates the versatility of percentage calculations using decimal representation.
Method 3: Using Proportions
We can set up a proportion to solve for the unknown part:
50/100 = x/70
Cross-multiplying, we get:
100x = 50 * 70 100x = 3500 x = 3500 / 100 x = 35
This method provides a structured approach suitable for more complex percentage problems.
Practical Applications of Percentages: Beyond the Basics
The seemingly simple calculation of 50 percent of 70 extends to numerous real-world applications across diverse fields. Let's explore some examples:
1. Finance and Budgeting:
- Discounts and Sales: Stores often offer discounts expressed as percentages. Understanding percentages allows you to quickly calculate the actual price reduction and the final price you'll pay. For instance, a 50% discount on a $70 item results in a saving of $35.
- Interest Rates: Interest rates on loans and savings accounts are typically expressed as percentages. Calculating the interest earned or paid requires a sound understanding of percentage calculations.
- Taxes: Taxes, such as sales tax or income tax, are also often represented as percentages. Accurate tax calculations depend on proficiency in handling percentages.
- Investment Returns: Investors monitor their investment returns as percentages, allowing them to track the growth or decline of their portfolio.
2. Data Analysis and Statistics:
- Data Representation: Percentages are frequently used to represent data in graphs, charts, and tables. For example, a survey might show that 50 percent of respondents prefer a particular product.
- Probability and Statistics: Percentages play a key role in probability calculations, expressing the likelihood of events occurring.
- Statistical Significance: In statistical analysis, percentages are used to assess the significance of findings.
3. Everyday Life:
- Tipping in Restaurants: Calculating a tip (e.g., 15% or 20%) on a restaurant bill involves percentage calculations.
- Shopping and Sales: Comparing prices and identifying the best deals often requires an understanding of percentages.
- Recipe Scaling: Adjusting recipes to serve more or fewer people requires using percentages to change ingredient quantities proportionally.
4. Science and Engineering:
- Chemical Concentrations: The concentration of solutions in chemistry is often expressed as percentages (e.g., 50% solution).
- Efficiency Calculations: The efficiency of machines or processes is frequently expressed as a percentage.
- Error Analysis: Percentages are crucial in expressing and analyzing errors in measurements or calculations.
Advanced Percentage Calculations: Beyond the Basics
While finding 50 percent of 70 is straightforward, other percentage calculations can be more complex. Let’s delve into a few:
1. Finding the Percentage One Number Represents of Another:
Suppose you scored 35 out of 70 on a test. To find the percentage score, you would perform the following calculation:
(35 / 70) * 100 = 50%
2. Finding a Number When a Percentage is Given:
Imagine you want to find a number such that 50% of that number is 35. Here's the calculation:
35 / 0.5 = 70
3. Calculating Percentage Increase or Decrease:
To determine the percentage increase from 70 to 105:
((105 - 70) / 70) * 100 = 50%
Similarly, to find the percentage decrease from 70 to 35:
((70 - 35) / 70) * 100 = 50%
Mastering Percentages: Tips and Resources
Mastering percentages is essential for navigating various aspects of life. Here are some tips to enhance your understanding and proficiency:
- Practice Regularly: The more you practice solving percentage problems, the more confident and proficient you will become.
- Use Different Methods: Experiment with different methods (fraction equivalent, decimal conversion, proportions) to find the approach that best suits your understanding.
- Break Down Complex Problems: Divide complex problems into smaller, manageable steps to make them easier to solve.
- Utilize Online Calculators (for Verification): Online calculators can be used to verify your answers and check your understanding of the concept.
- Seek Additional Resources: Numerous online resources, tutorials, and educational materials are available to further improve your understanding of percentages.
In conclusion, while finding 50 percent of 70 may initially seem trivial, the underlying principles of percentage calculations have far-reaching applications. A solid grasp of these concepts is essential for success in various academic, professional, and personal endeavors. By mastering percentages, you equip yourself with a crucial tool for tackling a vast array of numerical challenges and making informed decisions in diverse real-world situations. Remember to practice regularly and explore different calculation methods to solidify your understanding and become a percentage pro!
Latest Posts
Latest Posts
-
How Many Hours Is 15 Years
May 25, 2025
-
What Is The Greatest Common Factor Of 15 And 45
May 25, 2025
-
What Is The Least Common Multiple Of 12 And 27
May 25, 2025
-
30 Days From Oct 11 2024
May 25, 2025
-
What Is 34 Divided By 2
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 50 Percent Of 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.