What Is 3/4 Divided By 1/2
listenit
May 24, 2025 · 5 min read
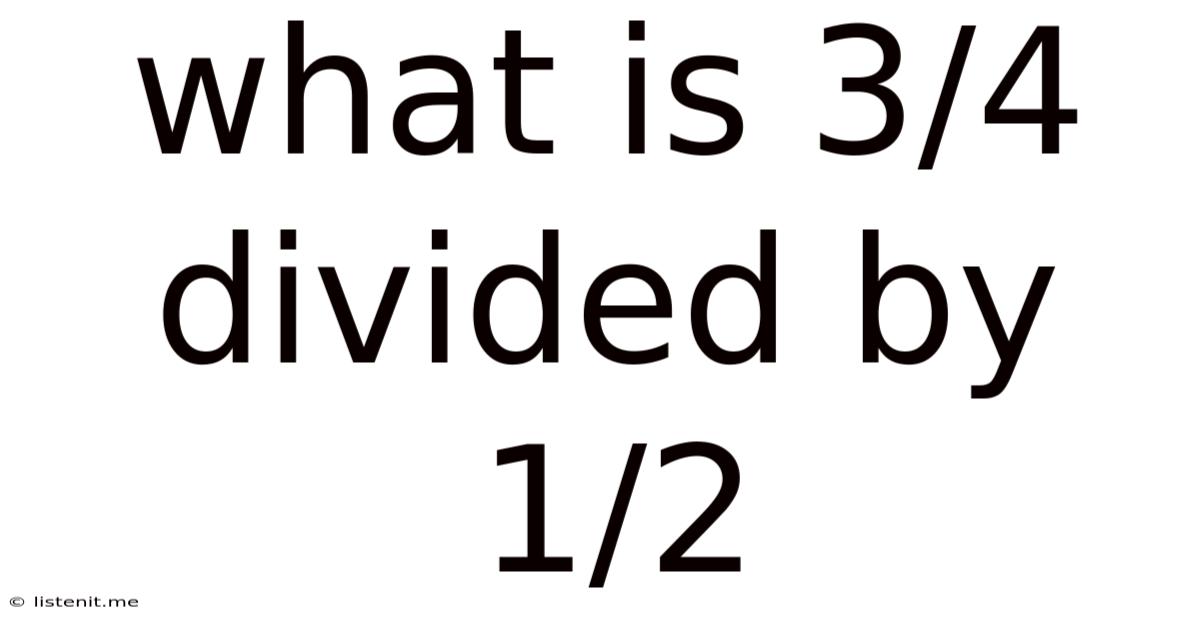
Table of Contents
What is 3/4 Divided by 1/2? A Deep Dive into Fraction Division
Understanding fraction division can be a stumbling block for many, but mastering it unlocks a world of mathematical possibilities. This comprehensive guide will not only answer the question "What is 3/4 divided by 1/2?" but also equip you with the knowledge and strategies to tackle any fraction division problem with confidence. We'll explore various methods, delve into the underlying principles, and provide practical examples to solidify your understanding.
Understanding Fraction Division: The "Keep, Change, Flip" Method
The most common and arguably easiest method for dividing fractions is the "keep, change, flip" (or "keep, switch, flip") method. Let's break it down step-by-step:
-
Keep: Keep the first fraction exactly as it is. In our example, this is 3/4.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip (or find the reciprocal of) the second fraction. The reciprocal of 1/2 is 2/1 (or simply 2).
Therefore, 3/4 ÷ 1/2 becomes 3/4 × 2/1.
Solving the Problem: 3/4 × 2/1
Now that we've transformed the division problem into a multiplication problem, the solution is straightforward:
- Multiply the numerators: 3 × 2 = 6
- Multiply the denominators: 4 × 1 = 4
This gives us the fraction 6/4.
Simplifying the Fraction: From 6/4 to 1 1/2
The fraction 6/4 is an improper fraction (the numerator is larger than the denominator). To simplify, we can convert it to a mixed number:
- Divide the numerator (6) by the denominator (4): 6 ÷ 4 = 1 with a remainder of 2.
- The whole number part of the mixed number is the quotient (1).
- The fractional part of the mixed number is the remainder (2) over the denominator (4): 2/4.
- Therefore, 6/4 simplifies to 1 2/4.
We can further simplify 2/4 by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 2. This results in 1/2.
Thus, the final, simplified answer is 1 1/2.
Alternative Methods for Dividing Fractions
While the "keep, change, flip" method is widely used and efficient, there are other ways to approach fraction division:
Method 2: Using Common Denominators
This method involves finding a common denominator for both fractions and then dividing the numerators. Let's apply it to our example:
-
Find a common denominator: The common denominator for 4 and 2 is 4.
-
Rewrite the fractions: 3/4 remains the same, and 1/2 becomes 2/4.
-
Divide the numerators: 3 ÷ 2 = 1.5 (Note: this results in a decimal, but we'll convert it to a fraction later)
-
Keep the common denominator: The denominator remains 4.
-
Convert the decimal to a fraction: 1.5 can be written as 3/2. So we get the fraction 3/2.
This gives us 3/2 or 1 1/2
This method, while effective, can be more time-consuming, especially when dealing with larger numbers or fractions with less obvious common denominators.
Method 3: Inverting and Multiplying (A more formal explanation)
This method provides a deeper understanding of why the "keep, change, flip" method works. Division is essentially the inverse operation of multiplication. Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal is simply the fraction turned upside down (numerator and denominator swapped).
Mathematically, a/b ÷ c/d = a/b × d/c.
In our example: 3/4 ÷ 1/2 = 3/4 × 2/1 = 6/4 = 1 1/2.
This method demonstrates the fundamental principle behind fraction division, solidifying the understanding of the "keep, change, flip" shortcut.
Practical Applications and Real-World Examples
Understanding fraction division is crucial in various real-world scenarios:
-
Cooking and Baking: Scaling recipes up or down requires dividing fractions. For example, if a recipe calls for 1/2 cup of flour and you want to make only half the recipe, you'll need to calculate 1/2 ÷ 2.
-
Sewing and Crafting: Cutting fabric or other materials accurately often involves dividing fractions to determine the correct measurements.
-
Construction and Engineering: Precision in construction and engineering relies heavily on accurate calculations involving fractions. Dividing fractions helps in determining the proportions of materials and components.
-
Data Analysis: Data analysis often involves working with fractions and percentages; understanding fraction division helps accurately interpret the data and draw meaningful conclusions.
Troubleshooting Common Mistakes in Fraction Division
Several common errors can occur when dividing fractions. Let's address them:
-
Forgetting to flip the second fraction: This is a very frequent mistake. Always remember the crucial "flip" step in the "keep, change, flip" method.
-
Incorrectly multiplying or simplifying: Careless mistakes in multiplication or simplification can lead to inaccurate results. Double-check your calculations to avoid errors.
-
Confusing division with addition or subtraction: Fraction division is distinct from fraction addition and subtraction; the operations and procedures differ significantly. Pay close attention to the operation sign.
-
Not simplifying the final answer: Always simplify your answer to its lowest terms to present the most concise and accurate solution.
Advanced Fraction Division Problems and Tips
Once you've mastered the basics, you can tackle more complex fraction division problems. These may involve mixed numbers, decimals within fractions, or a combination of both. Remember to:
-
Convert mixed numbers to improper fractions: Before performing any division, convert mixed numbers into improper fractions to simplify calculations.
-
Convert decimals to fractions: Similarly, convert decimals to fractions for consistent calculations.
-
Break down complex problems into smaller steps: Divide large or complex problems into smaller, manageable parts to improve clarity and reduce errors.
-
Practice regularly: The more you practice, the more comfortable and proficient you'll become in dividing fractions.
Conclusion: Mastering Fraction Division for Mathematical Success
Dividing fractions is a fundamental skill in mathematics, with applications extending far beyond the classroom. By understanding the underlying principles, mastering the various methods, and practicing regularly, you can confidently tackle any fraction division problem and unlock a greater understanding of the mathematical world. Remember the "keep, change, flip" method as your go-to strategy, but also explore the alternative approaches to solidify your grasp of this essential concept. With patience and practice, mastering fraction division will become second nature. The answer to "What is 3/4 divided by 1/2?" is 1 1/2, and now you understand the why behind it, empowering you to tackle any similar problems with ease and confidence.
Latest Posts
Latest Posts
-
What Percent Is 50 Out Of 70
May 24, 2025
-
30 Days After October 16 2024
May 24, 2025
-
How Old Would You Be If Born In 1989
May 24, 2025
-
What Is 25 Percent Of 450
May 24, 2025
-
25 7 Is What Percent Of 141
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 Divided By 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.