What Is 25 Percent Of 450
listenit
May 24, 2025 · 4 min read
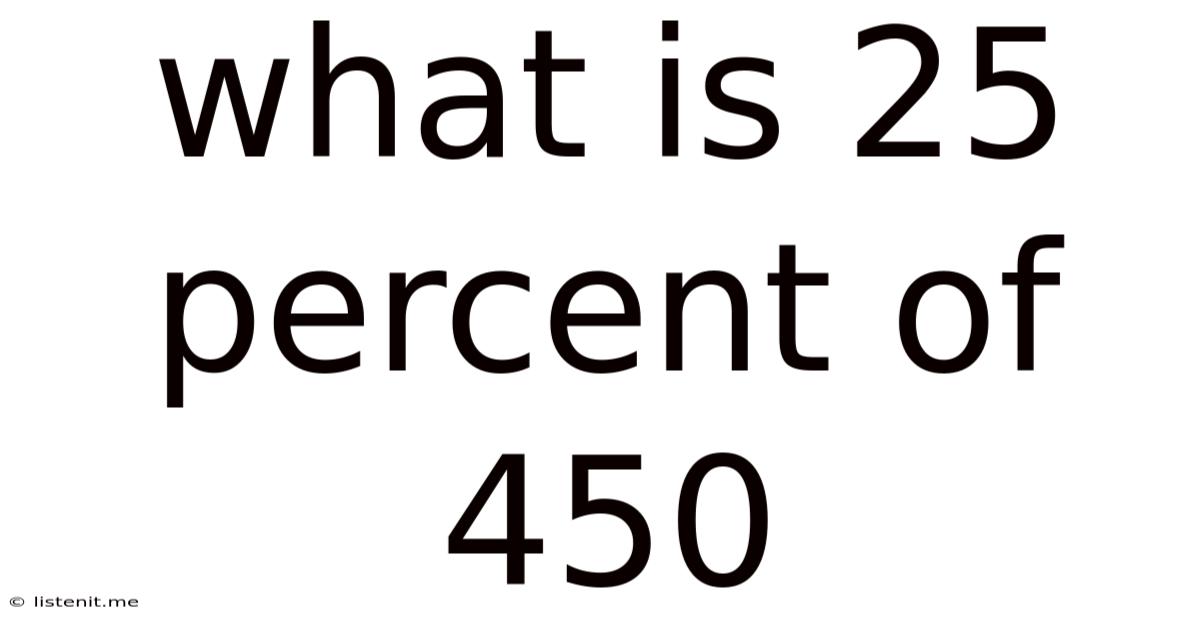
Table of Contents
What is 25 Percent of 450? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to calculate percentages allows for quick estimations, accurate comparisons, and informed decision-making. This comprehensive guide will walk you through the process of determining what 25 percent of 450 is, while exploring different methods and offering practical applications.
Understanding Percentages
Before delving into the calculation, let's establish a clear understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 25% means 25 out of 100, which can also be represented as the fraction 25/100 or the decimal 0.25.
Method 1: Using the Decimal Equivalent
This is perhaps the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the given number.
1. Convert the percentage to a decimal:
25% = 25/100 = 0.25
2. Multiply the decimal by the number:
0.25 * 450 = 112.5
Therefore, 25% of 450 is 112.5.
This method is efficient and easily adaptable to different percentages and numbers. It's particularly useful when using calculators or spreadsheets.
Method 2: Using the Fraction Equivalent
This method utilizes the fractional representation of the percentage.
1. Convert the percentage to a fraction:
25% = 25/100
2. Simplify the fraction (if possible):
25/100 simplifies to 1/4
3. Multiply the fraction by the number:
(1/4) * 450 = 450/4 = 112.5
Again, we arrive at the answer: 25% of 450 is 112.5. This method emphasizes the underlying mathematical relationship and can be helpful in understanding the proportional relationship between the percentage and the whole number.
Method 3: The Proportion Method
This method utilizes the concept of proportions to solve for the unknown value. We can set up a proportion:
25/100 = x/450
Where 'x' represents the unknown value (25% of 450).
To solve for x, we cross-multiply:
25 * 450 = 100 * x
11250 = 100x
x = 11250 / 100
x = 112.5
This confirms that 25% of 450 is 112.5. This method is valuable for understanding the proportional relationship between the percentage, the part, and the whole.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is vital in numerous real-world situations. Here are some examples:
1. Sales and Discounts:
Imagine a store offering a 25% discount on a $450 item. Using our calculations, you can quickly determine the discount amount ($112.50) and the final price ($450 - $112.50 = $337.50).
2. Tax Calculations:
If a sales tax is 25%, calculating the tax amount on a $450 purchase is identical to the problem at hand. The tax would be $112.50.
3. Tip Calculations:
In many cultures, it's customary to tip service providers. If you want to leave a 25% tip on a $450 restaurant bill, the tip amount would be $112.50.
4. Commission Calculations:
Salespeople often earn a commission based on a percentage of their sales. If a salesperson earns a 25% commission on $450 worth of sales, their commission would be $112.50.
5. Financial Analysis:
In finance, percentage calculations are crucial for understanding growth rates, returns on investment, and various other financial metrics. For example, if an investment grows by 25% from an initial investment of $450, the increase would be $112.50.
6. Scientific and Statistical Applications:
Percentage calculations are frequently used in scientific studies and statistical analyses to represent proportions, changes, and relationships between different variables.
Beyond the Basics: Working with Different Percentages
While we've focused on 25%, the same methods can be applied to calculate any percentage of any number. For example:
- To find 10% of 450: 0.10 * 450 = 45
- To find 50% of 450: 0.50 * 450 = 225
- To find 75% of 450: 0.75 * 450 = 337.5
- To find 1% of 450: 0.01 * 450 = 4.5
Advanced Percentage Calculations: Finding the Original Value
Sometimes, you know the percentage and the resulting value, but need to find the original value. For example, if 25% of a number is 112.5, what is the original number? To solve this, we can use the following formula:
Original Number = (Percentage Value / Percentage) * 100
In our example:
Original Number = (112.5 / 25) * 100 = 450
This demonstrates the reverse calculation, which is equally important in many practical scenarios.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill that extends beyond the classroom. The methods described—using decimal equivalents, fractions, and proportions—offer versatility and adaptability for various situations. Whether calculating discounts, taxes, tips, or interpreting financial data, a solid grasp of percentages enables informed decision-making and problem-solving in both personal and professional contexts. Remember that consistent practice and understanding the underlying mathematical principles will build your confidence and accuracy in handling percentage calculations. This thorough understanding equips you with the skills to tackle more complex percentage-related problems with ease.
Latest Posts
Latest Posts
-
What Is The Gcf Of 34 And 85
May 24, 2025
-
Greatest Common Factor Of 45 And 30
May 24, 2025
-
November 9 2024 Day Of The Week
May 24, 2025
-
24 To The Power Of 3
May 24, 2025
-
What Percent Of 350 Is 50
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Percent Of 450 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.