What Percent Is 50 Out Of 70
listenit
May 24, 2025 · 4 min read
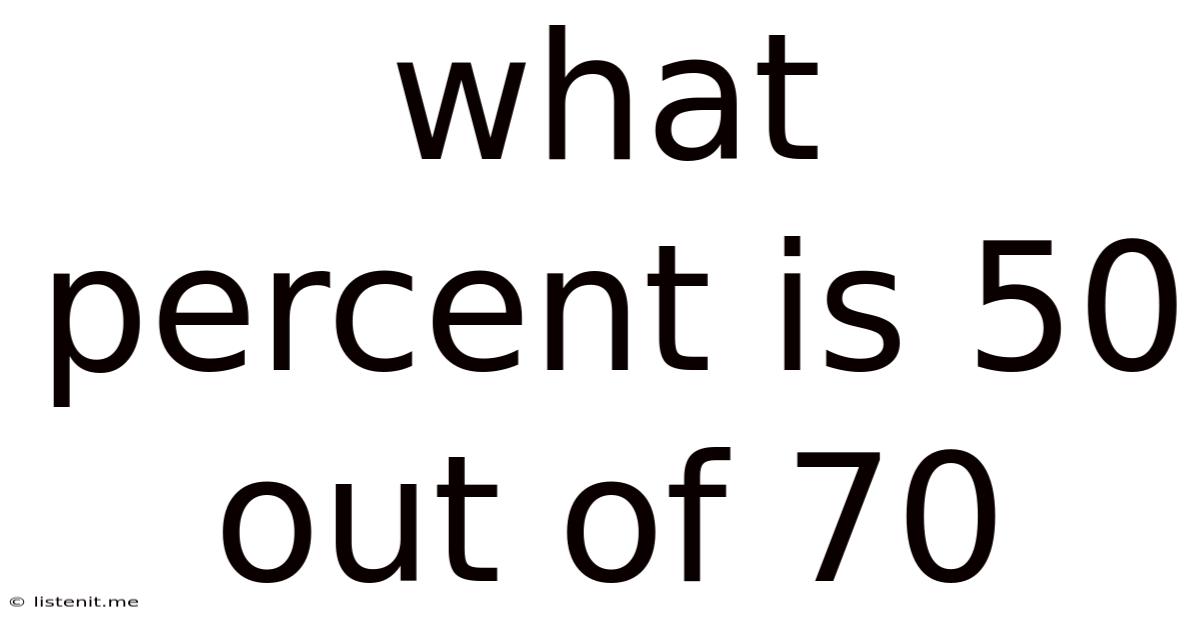
Table of Contents
What Percent is 50 Out of 70? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in everyday life, from understanding sales discounts and calculating grades to analyzing financial data and comprehending statistical information. This comprehensive guide will delve into the question, "What percent is 50 out of 70?", providing a step-by-step solution, exploring different calculation methods, and offering practical examples to solidify your understanding. We'll also touch upon related percentage problems and techniques to enhance your overall proficiency.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Percentages are a convenient way to represent proportions, making comparisons and interpretations easier than using fractions or decimals.
Method 1: The Basic Formula
The most straightforward method for calculating percentages involves a simple formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 50
- Whole: 70
Plugging these values into the formula:
(50 / 70) x 100% = 71.43% (approximately)
Therefore, 50 out of 70 is approximately 71.43%.
Method 2: Using Decimal Equivalents
This method involves converting the fraction to a decimal before multiplying by 100%.
- Divide the part by the whole: 50 / 70 = 0.7142857...
- Multiply the decimal by 100%: 0.7142857... x 100% = 71.43% (approximately)
This method provides the same result as the basic formula. The slight difference in the last decimal place might occur due to rounding during the decimal conversion.
Method 3: Proportion Method
The proportion method sets up a proportion to solve for the unknown percentage. This method is particularly useful for more complex percentage problems.
We can set up the proportion as follows:
50/70 = x/100
To solve for x (the percentage), we cross-multiply:
70x = 5000
x = 5000/70
x ≈ 71.43
Therefore, 50 out of 70 is approximately 71.43%.
Practical Applications and Examples
Understanding percentage calculations is crucial in numerous real-world scenarios. Here are a few examples:
-
Academic Performance: If a student scored 50 out of 70 marks on a test, their percentage score is 71.43%. This allows for easy comparison of performance across different tests and subjects.
-
Sales and Discounts: A store offering a 30% discount on an item originally priced at $70 would reduce the price by (30/100) * $70 = $21. The final price would be $70 - $21 = $49. Conversely, if an item is discounted to $49 from $70, the percentage discount can be calculated using the methods discussed above.
-
Financial Analysis: Percentage change calculations are fundamental in analyzing financial data, such as the growth of investments, fluctuations in stock prices, and changes in revenue. For example, if a company's profits increased from $50 million to $70 million, the percentage increase would be calculated as ((70-50)/50) * 100% = 40%.
-
Statistical Analysis: Percentages are widely used in statistics to represent proportions within datasets. For instance, if a survey of 70 people reveals that 50 prefer a particular product, the percentage of people preferring that product is 71.43%.
Rounding and Precision
When dealing with percentages, rounding is often necessary to present the result in a clear and concise manner. The level of precision required depends on the context. For instance, in financial calculations, greater precision might be necessary, while in informal settings, rounding to the nearest whole number might suffice. In the example of 50 out of 70, rounding to two decimal places (71.43%) is generally appropriate for many applications.
Dealing with More Complex Percentage Problems
While the basic percentage formula suffices for many scenarios, more complex problems may require additional steps. For example:
-
Finding the whole when the percentage and part are known: If 20% of a number is 10, what is the number? We can set up the equation: 0.20x = 10. Solving for x gives x = 50.
-
Finding the percentage increase or decrease: This involves calculating the difference between two numbers and expressing it as a percentage of the original number. For example, if a quantity increases from 60 to 80, the percentage increase is ((80-60)/60) x 100% = 33.33%.
-
Calculating compound interest: Compound interest involves earning interest on both the principal amount and accumulated interest. This requires iterative calculations, often using exponential functions.
Improving Your Percentage Calculation Skills
Practice is key to mastering percentage calculations. Start with simple problems and gradually progress to more complex ones. Using online calculators can be helpful for checking your answers and gaining confidence, but understanding the underlying principles is crucial for problem-solving. Explore different methods of calculation to find the one that best suits your learning style and the nature of the problem at hand.
Conclusion: Mastering the Art of Percentages
The ability to calculate percentages accurately and efficiently is an invaluable skill applicable across diverse fields. Understanding the underlying principles, along with mastering different calculation methods, allows you to tackle a wide range of percentage problems confidently. Whether you're calculating grades, analyzing financial data, or simply understanding discounts in a store, the knowledge gained from this guide will empower you to confidently navigate the world of percentages. Remember to practice regularly to enhance your skills and ensure accuracy. The ability to swiftly and accurately calculate percentages significantly enhances problem-solving capabilities and decision-making in various aspects of life.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 10 And 35
May 24, 2025
-
What Month Will It Be In 7 Months
May 24, 2025
-
What Is 30 Percent Off 70 Dollars
May 24, 2025
-
How Many Mph Is 120 Kmh
May 24, 2025
-
5 Out Of 22 As A Percentage
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 50 Out Of 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.