Is The Square Root Of 16 A Rational Number
listenit
Apr 06, 2025 · 5 min read
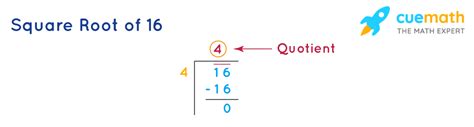
Table of Contents
Is the Square Root of 16 a Rational Number? A Deep Dive into Rationality and Irrationality
The question, "Is the square root of 16 a rational number?" might seem deceptively simple at first glance. However, it opens the door to a fascinating exploration of fundamental mathematical concepts: rational numbers, irrational numbers, and the very nature of numbers themselves. This article will not only answer the question definitively but also delve into the broader context of number classification, providing a comprehensive understanding for both beginners and those seeking a deeper appreciation of mathematical principles.
Understanding Rational Numbers
Before tackling the square root of 16, let's establish a clear definition of a rational number. A rational number is any number that can be expressed as a fraction p/q, where 'p' and 'q' are integers (whole numbers), and 'q' is not equal to zero. The key here is the ability to represent the number as a ratio of two integers.
Examples of rational numbers include:
- 1/2: A simple fraction.
- 3/4: Another common fraction.
- -5/7: Negative fractions are also rational.
- 2: Can be expressed as 2/1. All integers are rational.
- 0.75: This decimal can be expressed as 3/4.
- -2.5: This can be expressed as -5/2.
Understanding Irrational Numbers
In contrast to rational numbers, irrational numbers cannot be expressed as a simple fraction of two integers. Their decimal representations are non-terminating (they don't end) and non-repeating (they don't have a pattern that repeats infinitely).
Famous examples of irrational numbers include:
- π (pi): The ratio of a circle's circumference to its diameter, approximately 3.14159...
- e (Euler's number): The base of the natural logarithm, approximately 2.71828...
- √2 (the square root of 2): Approximately 1.41421... This is a classic example; it can be proven that √2 cannot be expressed as a fraction of two integers.
Calculating the Square Root of 16
Now, let's address the core question: Is √16 a rational number? The square root of a number is a value that, when multiplied by itself, equals the original number. In this case, we're looking for a number that, when multiplied by itself, equals 16.
That number is 4. Since 4 x 4 = 16, the square root of 16 is 4.
Is 4 a Rational Number?
The question now becomes: Is 4 a rational number? Absolutely! We can express 4 as a fraction: 4/1. It satisfies the definition of a rational number: it's a ratio of two integers (4 and 1), and the denominator (1) is not zero.
Therefore, the answer is YES!</h2>
The square root of 16, which is 4, is definitively a rational number.
Expanding on the Concepts: Further Exploration of Rationality and Irrationality
This seemingly simple problem provides a springboard to explore more complex mathematical ideas. Let's examine some related concepts:
Decimal Representations: A Key Distinguishing Feature
One crucial way to distinguish between rational and irrational numbers is through their decimal representations. Rational numbers have decimal representations that either:
- Terminate: They end after a finite number of digits (e.g., 0.75, 0.5).
- Repeat: They have a sequence of digits that repeats infinitely (e.g., 1/3 = 0.3333..., 1/7 = 0.142857142857...).
Irrational numbers, on the other hand, have decimal representations that are both non-terminating and non-repeating. This infinite, non-repeating nature is what makes them impossible to express as a simple fraction.
Proof by Contradiction: Demonstrating Irrationality
Proving that a number is irrational often involves a technique called "proof by contradiction." This method assumes the opposite of what you want to prove and then shows that this assumption leads to a logical contradiction. This contradiction implies that the initial assumption must be false, thus proving the original statement. The classic proof of the irrationality of √2 uses this method.
The Density of Rational and Irrational Numbers
A fascinating aspect of real numbers is the density of both rational and irrational numbers. This means that between any two distinct real numbers, you can always find both a rational number and an irrational number. This highlights the interwoven nature of these number types within the broader real number system.
Applications of Rational and Irrational Numbers
Rational and irrational numbers have widespread applications in various fields:
- Engineering and Physics: Rational numbers are commonly used in calculations and measurements where precision to a certain level is sufficient. Irrational numbers, such as π, are crucial in geometry and calculations involving circles and spheres.
- Computer Science: While computers work with approximations of irrational numbers, understanding their properties is vital for algorithms and data structures.
- Finance: Rational numbers are fundamental in financial calculations, dealing with currency, interest rates, and investments.
Conclusion: Beyond the Simple Answer
While the initial question, "Is the square root of 16 a rational number?" has a straightforward answer (yes), exploring the underlying concepts of rational and irrational numbers reveals a rich mathematical landscape. Understanding the differences between these number types, their decimal representations, and the methods used to prove their properties provides a deeper understanding of the foundations of mathematics and its widespread applications in various fields. This exploration underscores the importance of not just finding answers, but also comprehending the underlying principles that govern them. The journey from a simple square root calculation to an appreciation of the nuances of number theory is a testament to the beauty and complexity of mathematics.
Latest Posts
Latest Posts
-
Common Factors Of 8 And 36
Apr 07, 2025
-
How Do You Factor X 3 125
Apr 07, 2025
-
What Is The Electron Configuration Of V
Apr 07, 2025
-
What Is The Charge Of An Ionic Compound
Apr 07, 2025
-
How Many Ounces In 1 8 Pound
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Is The Square Root Of 16 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
