Common Factors Of 8 And 36
listenit
Apr 07, 2025 · 5 min read
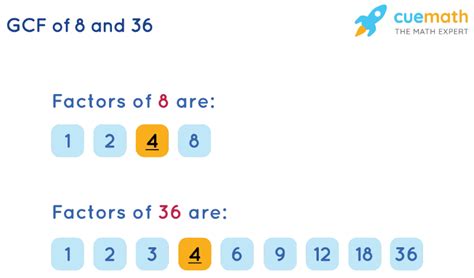
Table of Contents
Unveiling the Secrets: A Deep Dive into the Common Factors of 8 and 36
Finding the common factors of two numbers might seem like a simple arithmetic task, but it opens a door to understanding fundamental concepts in number theory, laying the groundwork for more advanced mathematical explorations. This article delves into the common factors of 8 and 36, exploring various methods to find them, examining their properties, and connecting these concepts to broader mathematical ideas. We'll go beyond a simple answer, offering a comprehensive understanding suitable for students, math enthusiasts, and anyone curious about the fascinating world of numbers.
Understanding Factors and Common Factors
Before we dive into the specifics of 8 and 36, let's establish a solid foundation. A factor of a number is a whole number that divides the number evenly without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12.
A common factor is a number that is a factor of two or more numbers. Identifying common factors is crucial in various mathematical applications, including simplifying fractions, finding the greatest common divisor (GCD), and solving problems involving divisibility.
Method 1: Listing Factors
The most straightforward method to find the common factors of 8 and 36 is to list all the factors of each number and then identify the ones they share.
Factors of 8:
1, 2, 4, 8
Factors of 36:
1, 2, 3, 4, 6, 9, 12, 18, 36
Comparing the two lists, we can see that the common factors of 8 and 36 are 1, 2, and 4.
Method 2: Prime Factorization
Prime factorization offers a more systematic and powerful approach to finding common factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Prime factorization involves expressing a number as a product of its prime factors.
Prime Factorization of 8:
8 = 2 x 2 x 2 = 2³
Prime Factorization of 36:
36 = 2 x 2 x 3 x 3 = 2² x 3²
To find the common factors, we identify the prime factors that both numbers share and their lowest powers. Both 8 and 36 share the prime factor 2. The lowest power of 2 present in both factorizations is 2².
Therefore, the common factors are derived from the shared prime factors:
- 2⁰ = 1
- 2¹ = 2
- 2² = 4
This method confirms that the common factors of 8 and 36 are 1, 2, and 4. This method is particularly useful when dealing with larger numbers where listing all factors becomes cumbersome.
Method 3: Euclidean Algorithm
The Euclidean algorithm provides an efficient way to find the greatest common divisor (GCD) of two numbers. The GCD is the largest common factor. Once we have the GCD, we can find all other common factors.
The Euclidean algorithm works by repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's apply the Euclidean algorithm to 8 and 36:
- Divide 36 by 8: 36 = 4 x 8 + 4
- Divide 8 by the remainder 4: 8 = 2 x 4 + 0
The last non-zero remainder is 4, so the GCD of 8 and 36 is 4.
Since 4 is the greatest common factor, all other common factors will be divisors of 4. The divisors of 4 are 1, 2, and 4. Thus, we confirm again that the common factors of 8 and 36 are 1, 2, and 4.
Beyond the Common Factors: Exploring Related Concepts
Understanding the common factors of 8 and 36 provides a springboard to explore related mathematical concepts:
Greatest Common Divisor (GCD)
As we've seen, the GCD of 8 and 36 is 4. The GCD plays a vital role in simplifying fractions and solving various mathematical problems. For example, to simplify the fraction 36/8, we divide both the numerator and denominator by their GCD (4), resulting in the simplified fraction 9/2.
Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest positive integer that is divisible by both numbers. While not directly derived from common factors, the GCD and LCM are closely related. The product of the GCD and LCM of two numbers equals the product of the two numbers.
In our case:
- GCD(8, 36) = 4
- LCM(8, 36) = 72
Notice that 8 x 36 = 288, and 4 x 72 = 288. This relationship provides a useful shortcut for finding the LCM if you already know the GCD.
Applications in Real-World Problems
The concept of common factors has practical applications beyond the realm of pure mathematics. Consider scenarios involving:
- Grouping items: Imagine you have 8 apples and 36 oranges. You want to create groups containing equal numbers of apples and oranges. The common factors (1, 2, and 4) represent the possible group sizes.
- Measurement conversions: Common factors simplify conversions between units of measurement.
- Scheduling events: Finding common factors can help in scheduling events that occur at regular intervals.
Conclusion: The Significance of Simple Arithmetic
While finding the common factors of 8 and 36 might seem elementary, it serves as a foundational building block in understanding more advanced mathematical concepts. The methods discussed—listing factors, prime factorization, and the Euclidean algorithm—offer diverse approaches to solving such problems, highlighting the versatility and power of basic number theory. The connections between common factors, GCD, and LCM emphasize the interconnectedness of mathematical ideas and demonstrate the relevance of these concepts in various real-world applications. By appreciating the seemingly simple act of finding common factors, we unlock a deeper understanding of the rich tapestry of mathematics. The seemingly simple task of finding the common factors of 8 and 36 unlocks a gateway to a world of mathematical exploration and discovery, demonstrating the power and beauty of numbers. Further exploration into these concepts can lead to a deeper appreciation for the elegance and interconnectedness of mathematical principles.
Latest Posts
Latest Posts
-
How Many Electrons Are In Mg 2
Apr 07, 2025
-
Whats 3 5 As A Decimal
Apr 07, 2025
-
In Glycolysis What Is Oxidized And What Is Reduced
Apr 07, 2025
-
A Word That Describes Or Modifies A Noun
Apr 07, 2025
-
What Stores Food And Water In A Cell
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Common Factors Of 8 And 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.