How Much Is A Triangle In Degrees
listenit
Mar 29, 2025 · 6 min read
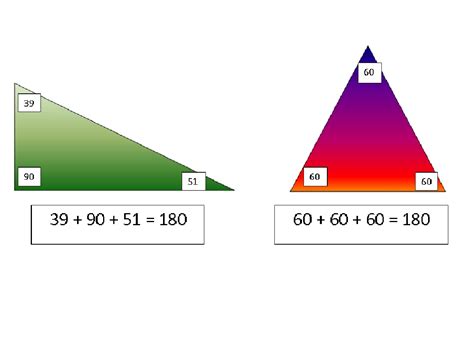
Table of Contents
How Much is a Triangle in Degrees? Understanding Angles and Their Properties
The simple question, "How much is a triangle in degrees?" unveils a fundamental concept in geometry: the sum of interior angles in any triangle always equals 180 degrees. This seemingly straightforward statement underpins countless geometric proofs, calculations, and applications in various fields, from architecture and engineering to computer graphics and cartography. Let's delve deeper into this core principle and explore its implications.
Understanding Angles in Triangles
Before we dive into the proof and applications, let's establish a clear understanding of what constitutes a triangle and its angles.
-
Triangle Definition: A triangle is a polygon with three sides and three angles. These sides can be of varying lengths, leading to different types of triangles (equilateral, isosceles, scalene). The angles, formed by the intersection of two sides, are the focus of our discussion.
-
Types of Angles:
- Acute Angle: An angle less than 90 degrees.
- Right Angle: An angle exactly equal to 90 degrees.
- Obtuse Angle: An angle greater than 90 degrees but less than 180 degrees.
-
Interior vs. Exterior Angles: The angles inside the triangle are called interior angles. Exterior angles are formed by extending one side of the triangle and measuring the angle formed outside the triangle. The sum of the exterior angles of any polygon, including a triangle, always equals 360 degrees. However, this article primarily focuses on interior angles.
Proving the 180-Degree Rule: Multiple Approaches
The assertion that the sum of interior angles in a triangle equals 180 degrees isn't just a postulate; it's a theorem proven through various geometric methods. Let's explore two common approaches:
1. Parallel Line Proof
This method leverages the properties of parallel lines and transversal lines.
- Draw a Triangle: Start with any triangle, ABC.
- Draw a Parallel Line: Draw a line through point C parallel to side AB.
- Identify Angles: Notice that the parallel line creates several angles. The angles on the same side of the transversal (the line segment AC) are supplementary (they add up to 180 degrees).
- Angle Relationships: Observe that angle ∠BAC is equal to the alternate interior angle formed by the parallel line and transversal AC. Similarly, ∠ABC is equal to the alternate interior angle formed by the parallel line and transversal BC.
- Summation: The three angles ∠BAC, ∠ABC, and the angle at C now sum up to 180 degrees (since they are supplementary angles). Since the first two angles are equivalent to the angles in our original triangle, the sum of the angles in triangle ABC equals 180 degrees.
2. Rotation Proof
This proof uses the concept of rotation around a point.
- Draw a Triangle: Begin with any triangle ABC.
- Rotate the Triangle: Rotate triangle ABC by 180 degrees about the midpoint of side AB.
- Observe the Angles: This rotation creates a new triangle, which forms a straight line with side AB of the original triangle.
- Summation: Since a straight line has an angle of 180 degrees, the three angles of the triangle ABC add up to 180 degrees.
Applications of the 180-Degree Rule
The 180-degree rule is not merely a theoretical concept; it has practical applications across numerous fields.
1. Surveying and Land Measurement
Surveyors rely heavily on this principle to accurately measure land areas. By measuring angles and distances, they can construct accurate maps and determine property boundaries. The 180-degree rule ensures the internal consistency of their measurements.
2. Construction and Architecture
In construction and architecture, understanding the angles of triangles is crucial for structural stability and design. Calculations involving roof pitches, angles of walls, and support structures all depend on this fundamental principle.
3. Navigation and GPS
GPS systems and navigational technologies utilize triangulation to determine location. By measuring angles to known points (satellites), the system calculates the user's position based on the intersection of the triangle formed. The accuracy of this process relies heavily on the precise angle measurements and the application of the 180-degree rule.
4. Computer Graphics and Game Development
Computer graphics and game development extensively use triangles in rendering and modeling. Polygons are often broken down into triangles for easier processing, and the 180-degree rule ensures that these triangles are correctly represented and rendered.
5. Engineering and Physics
Many engineering and physics problems involve calculations of forces, angles, and vectors. Understanding the angles within triangles is essential for solving problems related to equilibrium, stability, and motion analysis.
Types of Triangles and Their Angle Properties
The 180-degree rule applies to all types of triangles, but the specific angles vary depending on the side lengths:
1. Equilateral Triangles
An equilateral triangle has three equal sides and three equal angles. Since the sum of angles is 180 degrees, each angle in an equilateral triangle measures 60 degrees (180/3 = 60).
2. Isosceles Triangles
An isosceles triangle has two equal sides and two equal angles. The unequal angle is often referred to as the vertex angle.
3. Scalene Triangles
A scalene triangle has three unequal sides and three unequal angles.
Solving for Unknown Angles
The 180-degree rule provides a powerful tool for solving for unknown angles in a triangle. If you know two angles, you can easily find the third:
Example:
If two angles in a triangle are 45 degrees and 70 degrees, the third angle is:
180 degrees - 45 degrees - 70 degrees = 65 degrees
Exterior Angles and Their Relationship to Interior Angles
While the focus here is interior angles, understanding exterior angles is equally important. An exterior angle of a triangle is formed by extending one of its sides. The exterior angle and its adjacent interior angle are supplementary (add up to 180 degrees). Importantly, an exterior angle is also equal to the sum of the two opposite interior angles.
This relationship provides another method for solving for unknown angles within a triangle.
Beyond the Basics: Advanced Concepts
The 180-degree rule forms the foundation for more advanced geometric concepts, including:
- Trigonometry: The study of triangles and their relationships between angles and sides.
- Geometric Proofs: Many complex geometric proofs rely on the fundamental properties of triangles and the 180-degree rule.
- Non-Euclidean Geometry: While the 180-degree rule holds true in Euclidean geometry, it doesn't apply in all geometries. Understanding this rule in its context is key to grasping more advanced geometrical concepts.
Conclusion
The seemingly simple question, "How much is a triangle in degrees?" opens a vast world of geometrical principles and their applications. The 180-degree rule isn't just a fact; it's a fundamental theorem that underpins countless calculations and applications across various scientific and technological fields. Understanding this rule and its implications is crucial for anyone working with geometry, spatial reasoning, or fields that rely on precise measurements and calculations. From surveying land to designing buildings, navigating the globe to rendering 3D graphics, the 180-degree rule of triangles is a cornerstone of our understanding of the world around us.
Latest Posts
Latest Posts
-
Which Type Of Chemical Bond Involves The Exchange Of Electrons
Mar 31, 2025
-
What Is The Charge For Chlorine
Mar 31, 2025
-
Finding Mole Ratio Practice Questions 1 Answer Key
Mar 31, 2025
-
How Many Atoms Are In Nitrogen
Mar 31, 2025
-
How Many Valence Electrons Does Gallium Have
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How Much Is A Triangle In Degrees . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
