How Do You Simplify Cube Roots
listenit
Mar 31, 2025 · 5 min read
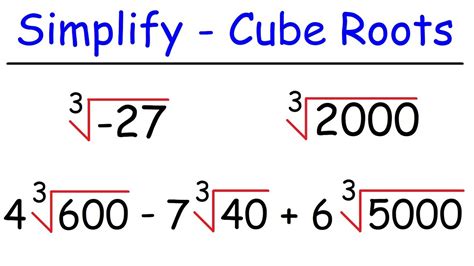
Table of Contents
How Do You Simplify Cube Roots? A Comprehensive Guide
Simplifying cube roots might seem daunting at first, but with a systematic approach and understanding of the underlying principles, it becomes a manageable and even enjoyable mathematical exercise. This comprehensive guide will walk you through various methods and techniques, equipping you with the skills to tackle cube root simplification with confidence. We'll cover everything from basic concepts to advanced strategies, ensuring you master this crucial aspect of algebra.
Understanding Cube Roots: The Fundamentals
Before diving into simplification techniques, let's solidify our understanding of what a cube root actually is. The cube root of a number is a value that, when multiplied by itself three times (cubed), results in the original number. We represent the cube root using the symbol ∛.
For example:
- ∛8 = 2 because 2 × 2 × 2 = 8
- ∛64 = 4 because 4 × 4 × 4 = 64
- ∛-27 = -3 because (-3) × (-3) × (-3) = -27
Key Point: The cube root of a negative number is a negative number. This differs from square roots, where the square root of a negative number is an imaginary number.
Method 1: Prime Factorization – The Cornerstone of Cube Root Simplification
Prime factorization is the most fundamental method for simplifying cube roots. It involves breaking down a number into its prime factors – numbers divisible only by 1 and themselves. Once we have the prime factorization, we can identify groups of three identical factors, which can then be "pulled out" of the cube root.
Steps:
-
Find the prime factorization: Break down the number inside the cube root into its prime factors. Use a factor tree or any method you're comfortable with.
-
Group factors in threes: Look for sets of three identical prime factors.
-
Extract the groups: For each group of three identical factors, bring one factor out of the cube root.
-
Leave remaining factors inside: Any factors that don't form a group of three remain inside the cube root.
Example: Simplify ∛108
-
Prime factorization: 108 = 2 × 2 × 2 × 3 × 3 × 3
-
Group factors in threes: (2 × 2 × 2) × (3 × 3 × 3)
-
Extract the groups: 2 × 3 = 6
-
Result: ∛108 simplifies to 6
Example with remaining factors: Simplify ∛54
-
Prime factorization: 54 = 2 × 3 × 3 × 3
-
Group factors in threes: 2 × (3 × 3 × 3)
-
Extract the groups: 3
-
Remaining factor: 2
-
Result: ∛54 simplifies to 3∛2
Method 2: Using Perfect Cubes – A Shortcut for Familiar Numbers
This method leverages your knowledge of perfect cubes (numbers that are the cubes of integers). By identifying perfect cube factors within the number under the cube root, you can simplify the expression more quickly.
Steps:
-
Identify perfect cube factors: Find perfect cubes that divide evenly into the number under the cube root. Common perfect cubes include 8, 27, 64, 125, 216, etc.
-
Rewrite the expression: Rewrite the number under the cube root as a product of the perfect cube factor and the remaining factor.
-
Simplify: Take the cube root of the perfect cube factor and leave the remaining factor inside the cube root.
Example: Simplify ∛250
-
Identify perfect cube factors: 250 = 125 × 2; 125 is a perfect cube (5³)
-
Rewrite the expression: ∛(125 × 2)
-
Simplify: ∛125 × ∛2 = 5∛2
Method 3: Simplifying Cube Roots with Variables
Simplifying cube roots involving variables follows a similar principle to simplifying numerical cube roots. We look for groups of three identical variables.
Steps:
-
Separate the numerical and variable parts: If the expression contains both numbers and variables, separate them.
-
Simplify the numerical part: Use prime factorization or the perfect cubes method to simplify the numerical cube root.
-
Simplify the variable part: For each variable, divide the exponent by 3. The quotient becomes the exponent of the variable outside the cube root, and the remainder (if any) remains inside the cube root.
Example: Simplify ∛(27x⁶y⁴)
-
Separate: ∛27 × ∛x⁶ × ∛y⁴
-
Simplify numerical part: ∛27 = 3
-
Simplify variable parts:
- ∛x⁶ = x^(6/3) = x²
- ∛y⁴ = y^(4/3) = y¹∛y (4 divided by 3 is 1 with a remainder of 1)
-
Result: 3x²y∛y
Method 4: Handling Fractions and Rationalizing the Denominator
When dealing with cube roots of fractions, we simplify both the numerator and the denominator separately. If there's a cube root in the denominator, we rationalize it by multiplying the numerator and denominator by a suitable expression to eliminate the cube root from the denominator.
Example: Simplify ∛(8/27)
-
Separate: ∛8 / ∛27
-
Simplify: 2 / 3
Example with rationalization: Simplify ∛(2/3)
-
Rewrite: ∛(2/3) = ∛2 / ∛3
-
Rationalize: To eliminate ∛3 in the denominator, multiply both numerator and denominator by ∛(3²) = ∛9
-
Simplify: (∛2 × ∛9) / (∛3 × ∛9) = ∛18 / 3
Advanced Techniques and Problem Solving Strategies
-
Combining Methods: Often, you'll need to combine multiple methods to fully simplify a complex cube root expression. Start with prime factorization and then leverage perfect cubes or variable simplification as needed.
-
Working with Negative Numbers: Remember that the cube root of a negative number is negative. This is important when simplifying expressions with negative numbers under the cube root.
Practice Problems
Now, let's test your newly acquired skills with a few practice problems:
- Simplify ∛1728
- Simplify ∛(64a³b⁶)
- Simplify ∛(5/16)
- Simplify ∛(-125x⁹y³)
- Simplify ∛(243x⁵y⁷)
Conclusion: Mastering Cube Root Simplification
Simplifying cube roots is a crucial algebraic skill. By mastering the techniques presented in this guide – prime factorization, using perfect cubes, handling variables, and rationalizing denominators – you'll be well-equipped to tackle a wide range of problems. Remember to practice regularly, and gradually you will build confidence and proficiency in simplifying cube roots. This comprehensive understanding will serve you well in more advanced mathematical concepts and problem-solving situations. Remember to break down complex problems into smaller, manageable steps and always double-check your work!
Latest Posts
Latest Posts
-
How Many Electrons Can The First Shell Hold
Apr 01, 2025
-
15 6 As A Mixed Number
Apr 01, 2025
-
What Two Monosaccharides Make Up Sucrose
Apr 01, 2025
-
The Heat Of Vaporization Of Water Is 40 66 Kj Mol
Apr 01, 2025
-
Why Are Hydrogen Bonds Important For Life
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How Do You Simplify Cube Roots . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
