Equilateral Triangle Inscribed In A Circle
listenit
Mar 29, 2025 · 5 min read
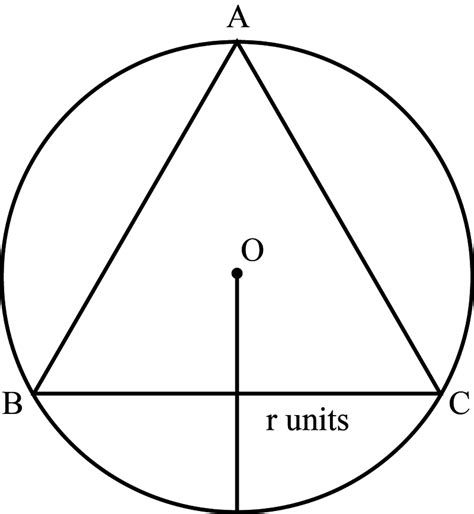
Table of Contents
Equilateral Triangles Inscribed in Circles: A Deep Dive into Geometry
The elegant relationship between an equilateral triangle and the circle circumscribing it has fascinated mathematicians and geometers for centuries. This seemingly simple geometric configuration holds a wealth of interesting properties and provides a fertile ground for exploring fundamental concepts in geometry, trigonometry, and even calculus. This article delves into the intricacies of an equilateral triangle inscribed in a circle, exploring its properties, derivations, and applications.
Understanding the Basics
Before diving into the deeper aspects, let's establish a foundational understanding. An equilateral triangle is a triangle with all three sides of equal length. This inherent symmetry leads to several other properties, including all three angles being equal (60 degrees each). A circumscribed circle, or circumcircle, is a circle that passes through all three vertices of a polygon. In this case, we are focusing on the circle that passes through all three vertices of our equilateral triangle.
The relationship between the equilateral triangle and its circumcircle is remarkably harmonious. The center of the circumcircle is also the centroid, circumcenter, incenter, and orthocenter of the equilateral triangle – a unique property not shared by other triangles. This means that the center of the circle is also the point where the medians, perpendicular bisectors, angle bisectors, and altitudes intersect.
Key Properties and Relationships
Several crucial relationships govern the dimensions and properties of an equilateral triangle inscribed in a circle:
1. Radius and Side Length Relationship
The most fundamental relationship is between the radius (R) of the circumcircle and the side length (a) of the equilateral triangle. This relationship can be derived using basic trigonometry. Consider one of the 60° angles subtended at the center of the circle by the side of the triangle. By applying the sine rule to the isosceles triangle formed by two radii and a side, we get:
a / sin(120°) = 2R
Since sin(120°) = √3/2, we simplify this to:
a = R√3
This equation reveals a direct proportionality between the side length of the equilateral triangle and the radius of its circumcircle. Knowing one, we can easily calculate the other.
2. Area Calculation
The area (A) of an equilateral triangle can be calculated using its side length:
A = (√3/4) * a²
Substituting the relationship between 'a' and 'R' from above, we get:
A = (3√3/4) * R²
This formula provides a direct method to calculate the area of the equilateral triangle using only the radius of the circumscribing circle.
3. Altitude and Radius
The altitude (h) of an equilateral triangle is the perpendicular distance from a vertex to the opposite side. The altitude, radius, and side length are related by:
h = (√3/2) * a = (3/2) * R
This demonstrates a direct proportionality between the altitude, radius, and side length of the equilateral triangle.
4. Inradius and Radius
The inradius (r) of a triangle is the radius of its incircle (the circle tangent to all three sides). For an equilateral triangle, the inradius is exactly half the circumradius:
r = R/2
This simple relationship highlights the inherent symmetry and balanced nature of the equilateral triangle.
Derivations and Proofs
The relationships mentioned above aren't arbitrary; they're derived through rigorous geometric and trigonometric proofs. Let's look at one example – deriving the relationship between the side length (a) and the radius (R):
Proof using Trigonometry:
-
Draw the equilateral triangle ABC inscribed in a circle with center O.
-
Draw radii OA, OB, and OC. These are all equal in length (R).
-
Consider triangle AOB. This is an isosceles triangle with OA = OB = R and angle AOB = 120° (because the angles subtended at the center are twice the angles at the circumference).
-
Apply the Law of Sines to triangle AOB:
a / sin(120°) = R / sin(30°)
- Substitute sin(120°) = √3/2 and sin(30°) = 1/2:
a / (√3/2) = R / (1/2)
- Solve for 'a':
a = R√3
This proof demonstrates the fundamental relationship between the side length and the radius of the circumcircle of an equilateral triangle. Similar rigorous proofs can be devised for the other relationships mentioned earlier.
Applications and Further Exploration
The study of equilateral triangles inscribed in circles extends beyond theoretical geometry. It finds applications in various fields:
-
Engineering and Design: The symmetric nature of this configuration is frequently exploited in structural design, particularly in creating stable and evenly distributed load-bearing structures.
-
Computer Graphics and Animation: The predictable geometry is useful in creating models and simulations in computer-aided design (CAD) and animation software. The simple calculations involved make it efficient for computer processing.
-
Art and Architecture: The elegant simplicity and inherent balance have influenced art and architecture for centuries. Many structures incorporate the equilateral triangle and its associated circle.
Furthermore, exploring the concept can lead to deeper mathematical inquiries:
-
Generalization to other polygons: The concepts explored here can be extended to investigate inscribed regular polygons and the relationships between their side lengths, radii, and areas.
-
Three-dimensional extensions: The idea can be extended into three dimensions, examining the relationships between regular tetrahedra and their circumscribing spheres.
-
Advanced mathematical concepts: The study of inscribed equilateral triangles can introduce more advanced concepts, such as coordinate geometry and vector calculus, providing a solid foundation for further mathematical exploration.
Conclusion
The seemingly simple geometry of an equilateral triangle inscribed in a circle unveils a rich tapestry of mathematical relationships and properties. The inherent symmetry and the elegant formulas connecting the side length, radius, area, and altitude provide fertile ground for geometric exploration and application across diverse fields. Understanding these relationships strengthens fundamental geometrical understanding and lays a foundation for further mathematical exploration. Whether for solving geometric problems, understanding structural design, or appreciating the beauty of mathematical symmetry, the insights gained from studying this configuration prove invaluable.
Latest Posts
Latest Posts
-
Compute And Interpret The Mean Of The Random Variable X
Apr 01, 2025
-
What Is At The Center Of Our Solar System
Apr 01, 2025
-
Calculating The Ph Of A Weak Acid Solution
Apr 01, 2025
-
Which Of The Following Is A Function Of Cell Membrane
Apr 01, 2025
-
Do Polar Substances Dissolve In Water
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Equilateral Triangle Inscribed In A Circle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
