Do Exponential Functions Have Vertical Asymptotes
listenit
Mar 31, 2025 · 5 min read
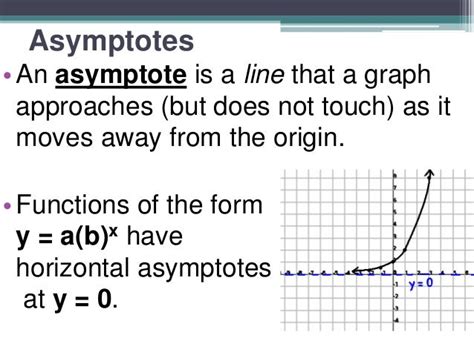
Table of Contents
Do Exponential Functions Have Vertical Asymptotes? A Comprehensive Exploration
Exponential functions, characterized by their rapid growth or decay, are fundamental in mathematics and numerous applications across diverse fields. Understanding their properties, including the presence or absence of asymptotes, is crucial for effective modeling and analysis. This in-depth article comprehensively explores the question: Do exponential functions have vertical asymptotes? The answer, while seemingly straightforward, requires a nuanced understanding of function behavior and the different forms exponential functions can take.
Understanding Exponential Functions and Their General Form
Before diving into asymptotes, let's establish a solid foundation by defining exponential functions. Generally, an exponential function is a function of the form:
f(x) = a<sup>x</sup>
where:
- a is a positive constant called the base (a > 0 and a ≠ 1).
- x is the exponent, which can be any real number.
The restriction on the base (a > 0 and a ≠ 1) is critical. If a = 1, the function becomes f(x) = 1, a constant function, and if a ≤ 0, the function becomes undefined for some real values of x (e.g., fractional exponents involving even denominators).
The key feature of an exponential function is that the independent variable, x, is in the exponent. This contrasts with power functions, where the independent variable is the base. This seemingly small difference leads to dramatically different growth characteristics.
Asymptotes: Horizontal and Vertical
Asymptotes are lines that a curve approaches arbitrarily closely, but never touches or crosses. There are two main types of asymptotes:
- Horizontal Asymptotes: These are horizontal lines that the function approaches as x approaches positive or negative infinity.
- Vertical Asymptotes: These are vertical lines that the function approaches as x approaches a specific value, often where the function is undefined.
Do Standard Exponential Functions Have Vertical Asymptotes?
Let's consider the standard exponential function: f(x) = a<sup>x</sup> (where a > 0 and a ≠ 1). This function is defined for all real numbers x. No matter how large or small x becomes, the function will always produce a real number result. There are no values of x for which the function is undefined.
Therefore, the standard exponential function f(x) = a<sup>x</sup> does not have any vertical asymptotes.
The graph of this function will always smoothly curve, extending infinitely in both the positive and negative y directions. It will approach, but never touch, the x-axis (y = 0) if 0 < a < 1 (exponential decay), or extend infinitely upwards if a > 1 (exponential growth).
Horizontal Asymptotes of Standard Exponential Functions
While lacking vertical asymptotes, standard exponential functions do possess horizontal asymptotes. The horizontal asymptote is determined by the base 'a' and the behavior of the function as x approaches positive or negative infinity:
- If a > 1: As x approaches negative infinity, f(x) approaches 0. Therefore, the horizontal asymptote is y = 0.
- If 0 < a < 1: As x approaches positive infinity, f(x) approaches 0. Therefore, the horizontal asymptote is y = 0.
Transformations and Modified Exponential Functions
The situation changes when we consider transformations of the basic exponential function. These transformations can introduce vertical asymptotes. Consider these examples:
1. Exponential Functions with Added or Subtracted Terms:
Adding or subtracting terms can shift the function vertically but does not introduce vertical asymptotes. For example:
g(x) = a<sup>x</sup> + c
This function is simply a vertical translation of f(x) = a<sup>x</sup> by 'c' units. It still has no vertical asymptotes.
2. Exponential Functions with Terms in the Exponent:
Introducing terms within the exponent can dramatically affect the function's behavior. For instance:
h(x) = a<sup>(x-b)</sup>
This is a horizontal translation of the basic exponential function. It still does not have vertical asymptotes.
However, consider the function:
i(x) = a<sup>(1/x)</sup>
In this case, the function becomes undefined at x = 0, because 1/x approaches infinity. As x approaches 0, a<sup>(1/x)</sup> either approaches 0 or infinity depending on whether a is greater than or less than 1. In this situation, the function has a vertical asymptote at x = 0.
3. Exponential Functions with Fractional Exponents Involving x in the Denominator:
Functions with expressions involving 'x' in the denominator within the exponent can lead to vertical asymptotes. For example:
j(x) = a<sup>(1/(x-k))</sup>
Here, the function is undefined when the denominator of the exponent (x - k) equals zero, meaning at x = k. As x approaches k, the exponent approaches either positive or negative infinity, leading to a vertical asymptote at x = k.
This demonstrates that introducing expressions involving the variable 'x' in the denominator of the exponent can result in a vertical asymptote.
Real-World Applications and the Implications of Asymptotes
Understanding asymptotes is crucial in various real-world applications of exponential functions:
- Population Growth: Modeling population growth often uses exponential functions. The horizontal asymptote might represent a carrying capacity, limiting population size.
- Radioactive Decay: Radioactive decay follows an exponential decay pattern. The horizontal asymptote signifies a minimal amount of remaining radioactive material.
- Compound Interest: Compound interest calculations frequently involve exponential functions. The function’s behavior, including any asymptotes, sheds light on long-term growth patterns.
- Spread of Diseases: Exponential functions can model the spread of contagious diseases. The asymptote might relate to the total number of susceptible individuals in a population.
- Learning Curves: Exponential functions can describe learning curves, where the rate of improvement diminishes over time. Asymptotes can represent upper limits of skill or knowledge attainment.
Conclusion: A Nuanced Understanding of Vertical Asymptotes in Exponential Functions
In conclusion, while a basic exponential function of the form f(x) = a<sup>x</sup> (where a > 0 and a ≠ 1) does not possess vertical asymptotes, modifications to this basic form, especially those involving 'x' in the denominator within the exponent, can introduce vertical asymptotes. The presence or absence of vertical asymptotes greatly depends on the specific structure and transformations applied to the exponential function. Understanding this nuance is essential for accurately interpreting and applying exponential functions across various fields. A thorough comprehension of exponential functions, including their asymptotes, is crucial for effectively using these powerful mathematical tools in modeling and solving real-world problems. Careful attention to the function's form and potential transformations is necessary for a precise analysis of its behavior and the identification of any asymptotes.
Latest Posts
Latest Posts
-
How Many Pi Electrons In A Double Bond
Apr 01, 2025
-
Number Of Valence Electrons In Silicon
Apr 01, 2025
-
What Is 2 9 In A Decimal
Apr 01, 2025
-
What Is 24 Divided By 4
Apr 01, 2025
-
Milk Turning Sour Is A Chemical Change
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Do Exponential Functions Have Vertical Asymptotes . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
