What Is 2/9 In A Decimal
listenit
Apr 01, 2025 · 5 min read
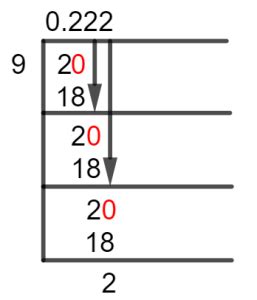
Table of Contents
What is 2/9 in Decimal? A Comprehensive Guide to Fraction to Decimal Conversion
Converting fractions to decimals is a fundamental skill in mathematics, with applications spanning various fields from everyday calculations to complex scientific computations. This comprehensive guide delves deep into the conversion of the fraction 2/9 into its decimal equivalent, exploring the underlying methods, providing practical examples, and addressing common misconceptions. We'll go beyond a simple answer and equip you with the knowledge to confidently tackle similar fraction-to-decimal conversions.
Understanding Fractions and Decimals
Before diving into the conversion of 2/9, let's solidify our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a part of a whole using a base-ten system, where the digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on.
The Relationship Between Fractions and Decimals
Fractions and decimals are fundamentally interchangeable; they both represent portions of a whole. Converting a fraction to a decimal involves expressing the fraction's ratio as a decimal number. This is done through division: the numerator is divided by the denominator.
Converting 2/9 to a Decimal
Now, let's tackle the conversion of the fraction 2/9 to its decimal equivalent. The process is straightforward:
-
Divide the numerator by the denominator: We divide 2 by 9.
-
Perform the long division: This is the most common method. You'll find that 9 doesn't divide evenly into 2. We add a decimal point and a zero to the 2, making it 2.0. Then we perform the long division:
9 | 2.0000...
0.222...
-
Interpret the result: The long division shows that 2/9 is equal to 0.222... The ellipsis (...) indicates that the digit 2 repeats infinitely.
Understanding Repeating Decimals
The decimal representation of 2/9, 0.222..., is an example of a repeating decimal or recurring decimal. Repeating decimals have a digit or a group of digits that repeat infinitely. These are often denoted by placing a bar over the repeating digits: 0.$\overline{2}$. This notation clearly indicates the repetition.
Why does 2/9 result in a repeating decimal?
The reason 2/9 results in a repeating decimal is because the denominator (9) contains prime factors other than 2 and 5. When the denominator of a fraction contains only prime factors of 2 and 5 (or is a multiple of those), the decimal representation will terminate (end). However, if the denominator contains any prime factors other than 2 and 5, the decimal representation will be a repeating decimal.
Alternative Methods for Converting Fractions to Decimals
While long division is the most common method, other techniques can be used to convert fractions to decimals. These alternative approaches can be particularly helpful in certain scenarios or for those seeking quicker solutions.
Using a Calculator
Most calculators have the functionality to directly convert fractions to decimals. Simply input the fraction as 2/9 and the calculator will display the decimal equivalent: 0.222... or 0.$\overline{2}$.
Using Equivalent Fractions with a Power of 10 Denominator
While not always possible, converting the fraction to an equivalent fraction with a denominator that's a power of 10 (10, 100, 1000, etc.) can be a shortcut. This method relies on finding a number to multiply both the numerator and denominator to achieve a power of 10. Unfortunately, this isn't feasible with 2/9 because 9 cannot be multiplied by an integer to create a power of 10.
Applications of Decimal Conversions
The ability to convert fractions to decimals has widespread applications in various fields:
- Finance: Calculating percentages, interest rates, and proportions.
- Engineering: Precision measurements and calculations.
- Science: Representing experimental data and results.
- Everyday life: Calculating tips, discounts, and proportions in recipes.
Practical Examples Using 2/9 in Decimal Form
Let's explore a few practical examples showcasing the use of 2/9 (0.$\overline{2}$) in real-world situations:
Example 1: Calculating a Discount
A store offers a 2/9 discount on an item priced at $27. To calculate the discount, we multiply the price by 2/9 (or 0.$\overline{2}$):
$27 * 0.$\overline{2}$ ≈ $6
(Note: Due to the repeating decimal, the result will be an approximation unless we utilize the fraction form for precise calculation.)
Example 2: Sharing Resources
Two friends want to share 9 cookies equally. Each friend gets 2/9 of the cookies. Expressing this as a decimal, each friend receives approximately 0.222 cookies. This might not be practically feasible to split the cookies, illustrating a limitation in using decimal approximations in this context.
Addressing Common Misconceptions
Several common misconceptions surround fraction-to-decimal conversions:
-
Rounding Errors: When dealing with repeating decimals, rounding can introduce inaccuracies. It's important to consider the level of precision required for a given application.
-
Confusing Terminating and Repeating Decimals: Remember that the nature of a fraction's decimal representation depends solely on the prime factorization of its denominator.
-
Over-reliance on Calculators: While calculators are helpful, understanding the underlying principles of conversion is crucial for solving problems and avoiding errors.
Conclusion
Converting the fraction 2/9 to its decimal equivalent (0.$\overline{2}$) involves a simple yet fundamental mathematical process. Understanding this conversion goes beyond merely obtaining the answer; it unlocks a deeper understanding of fractions, decimals, and their relationships. This knowledge empowers you to confidently tackle similar conversions and apply them in various real-world scenarios, reinforcing the importance of this essential mathematical skill. By mastering this process, you enhance your problem-solving abilities and broaden your mathematical comprehension. Furthermore, understanding the intricacies of repeating decimals and their significance provides a more comprehensive and nuanced grasp of the number system.
Latest Posts
Latest Posts
-
What Is 1 To The 5th Power
Apr 02, 2025
-
Takes The Place Of A Noun
Apr 02, 2025
-
What Is The Fraction Of 0 04
Apr 02, 2025
-
How Does The Use Of Fertilizer Affect The Nitrogen Cycle
Apr 02, 2025
-
Aluminum Has A Density Of 2 70 G Cm3
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/9 In A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
