What Is The Fraction Of 0.04
listenit
Apr 02, 2025 · 5 min read
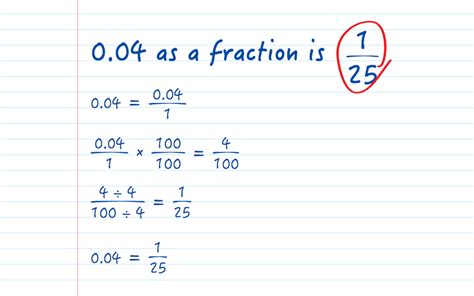
Table of Contents
What is the Fraction of 0.04? A Deep Dive into Decimal-to-Fraction Conversion
Understanding how to convert decimals to fractions is a fundamental skill in mathematics, crucial for various applications from basic arithmetic to advanced calculus. This comprehensive guide will delve into the process of converting the decimal 0.04 into a fraction, exploring the underlying principles and offering a range of approaches to tackle similar conversions. We'll also touch upon the broader context of decimal-fraction conversions and their importance.
Understanding Decimals and Fractions
Before we jump into the conversion, let's briefly recap what decimals and fractions represent.
Decimals: Decimals are a way of representing numbers that are not whole numbers. They use a base-ten system, with digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. For example, 0.04 represents four hundredths.
Fractions: Fractions represent a part of a whole. They are expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the number of equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered. For example, 1/2 represents one out of two equal parts.
Converting 0.04 to a Fraction: Step-by-Step
The conversion of 0.04 to a fraction involves several straightforward steps:
Step 1: Identify the Place Value
The decimal 0.04 has its last digit (4) in the hundredths place. This means that the decimal represents 4 hundredths.
Step 2: Write the Fraction
Based on the place value, we can write the fraction as 4/100. The numerator is the digit after the decimal point (4), and the denominator is 10 raised to the power of the number of decimal places (10² = 100).
Step 3: Simplify the Fraction (If Possible)
The fraction 4/100 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 4 and 100 is 4. Dividing both the numerator and denominator by 4, we get:
4 ÷ 4 = 1 100 ÷ 4 = 25
Therefore, the simplified fraction is 1/25.
Alternative Methods for Decimal-to-Fraction Conversion
While the above method is the most straightforward for 0.04, there are other methods that can be applied to more complex decimal conversions:
Method 1: Using the Place Value Directly
This method is particularly useful for decimals with a small number of decimal places. You directly write the decimal digits as the numerator and the appropriate power of 10 as the denominator. For example:
- 0.3 = 3/10
- 0.25 = 25/100
- 0.125 = 125/1000
Method 2: Long Division
This method is useful for recurring decimals and decimals with many decimal places. The process involves setting up a long division problem where the decimal is the dividend and a power of 10 is the divisor. The result is the fraction. However, this method might lead to complex fractions, particularly for recurring decimals.
Method 3: Multiplying by a Power of 10
This method involves multiplying the decimal by a power of 10 until you get a whole number. The power of 10 becomes the denominator of the fraction, and the whole number becomes the numerator. For instance, to convert 0.04 to a fraction:
- Multiply 0.04 by 100: 0.04 x 100 = 4
- The denominator is 100 (since we multiplied by 100).
- The fraction is 4/100, which simplifies to 1/25.
Practical Applications of Decimal-to-Fraction Conversion
The ability to convert decimals to fractions is essential in many areas, including:
- Basic Arithmetic: Solving problems involving fractions and decimals.
- Algebra: Manipulating algebraic expressions that involve fractions and decimals.
- Geometry: Calculating areas, volumes, and other geometric properties.
- Chemistry: Determining molar masses and other chemical calculations.
- Physics: Solving physics problems involving measurements and units.
- Engineering: Designing and building structures and machines.
- Finance: Calculating interest rates, percentages, and other financial metrics.
Understanding Recurring Decimals and their Fraction Equivalents
Recurring decimals are decimals with digits that repeat infinitely. Converting these to fractions requires a slightly different approach. Here’s a basic example:
Let's consider the recurring decimal 0.333... (where the 3 repeats infinitely). To convert this to a fraction:
- Let x = 0.333...
- Multiply both sides by 10: 10x = 3.333...
- Subtract the first equation from the second: 10x - x = 3.333... - 0.333...
- Simplify: 9x = 3
- Solve for x: x = 3/9
- Simplify the fraction: x = 1/3
This demonstrates that the recurring decimal 0.333... is equivalent to the fraction 1/3. Similar techniques can be used for other recurring decimals, although the process might become more complex depending on the repeating pattern.
Beyond 0.04: Practicing Decimal-to-Fraction Conversions
To solidify your understanding, practice converting other decimals to fractions. Start with simple decimals like 0.1, 0.5, 0.75, and gradually move to more complex ones. Remember to always simplify your fractions to their lowest terms. Here are some examples for practice:
- 0.2: This is 2/10 which simplifies to 1/5.
- 0.7: This is 7/10.
- 0.15: This is 15/100 which simplifies to 3/20.
- 0.625: This is 625/1000 which simplifies to 5/8.
- 0.375: This is 375/1000 which simplifies to 3/8.
Troubleshooting Common Mistakes
Common mistakes when converting decimals to fractions include:
- Incorrect Place Value Identification: Ensure you correctly identify the place value of the last digit in the decimal.
- Failure to Simplify: Always simplify the resulting fraction to its lowest terms.
- Errors in Arithmetic: Double-check your calculations to avoid errors in simplifying the fraction.
- Misunderstanding Recurring Decimals: Employ the appropriate techniques for converting recurring decimals to fractions.
Conclusion
Converting decimals to fractions is a fundamental skill in mathematics with broad applications. Understanding the underlying principles and practicing different conversion methods will build confidence and competence in tackling more complex mathematical problems. Remember that the process for 0.04, and other similar decimals, involves identifying the place value, writing the fraction, and then simplifying the fraction to its lowest terms. This comprehensive guide has explored the various methods and provided ample examples to aid your understanding and practice. Mastering this skill will significantly enhance your mathematical abilities across various disciplines.
Latest Posts
Latest Posts
-
What Is The Charge On A Potassium Ion
Apr 03, 2025
-
What Is The Symbol For Entropy
Apr 03, 2025
-
6 Less Than The Product Of 4 And X
Apr 03, 2025
-
What Planet Is The Closest Size To Earth
Apr 03, 2025
-
How Many Fl Oz In A Fifth
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Fraction Of 0.04 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
