What Is 1 To The 5th Power
listenit
Apr 02, 2025 · 5 min read
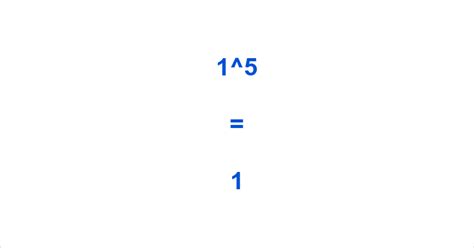
Table of Contents
What is 1 to the 5th Power? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 1 to the 5th power?" opens a door to a fascinating exploration of exponents, their properties, and their widespread applications across various fields of mathematics and beyond. While the answer itself is straightforward – 1 – the journey to understanding why this is the case provides valuable insights into fundamental mathematical concepts. This article will delve into the intricacies of exponents, explain the principle behind 1 raised to any power, and explore the broader significance of this seemingly simple calculation.
Understanding Exponents
Before tackling the specific problem of 1 raised to the 5th power, let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's represented by a superscript number placed to the right of the base. For example, in the expression 2³, the base is 2, and the exponent is 3. This means 2 multiplied by itself three times: 2 × 2 × 2 = 8.
Key Terminology:
- Base: The number being multiplied repeatedly.
- Exponent: The number indicating how many times the base is multiplied by itself.
- Power: Another term for exponent.
The Rules of Exponents
Several rules govern how exponents behave. Understanding these rules is crucial for working with exponential expressions efficiently and accurately. Some key rules include:
-
Product of Powers: When multiplying two numbers with the same base, add the exponents: a<sup>m</sup> × a<sup>n</sup> = a<sup>m+n</sup>. For example, 2² × 2³ = 2<sup>2+3</sup> = 2⁵ = 32.
-
Quotient of Powers: When dividing two numbers with the same base, subtract the exponents: a<sup>m</sup> ÷ a<sup>n</sup> = a<sup>m-n</sup>. For example, 3⁵ ÷ 3² = 3<sup>5-2</sup> = 3³ = 27.
-
Power of a Power: When raising a power to another power, multiply the exponents: (a<sup>m</sup>)<sup>n</sup> = a<sup>m×n</sup>. For example, (5²)³ = 5<sup>2×3</sup> = 5⁶ = 15625.
-
Power of a Product: When raising a product to a power, raise each factor to that power: (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>. For example, (2 × 3)² = 2² × 3² = 4 × 9 = 36.
-
Power of a Quotient: When raising a quotient to a power, raise both the numerator and the denominator to that power: (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>. For example, (4/2)² = 4²/2² = 16/4 = 4.
1 Raised to Any Power: The Special Case
Now, let's focus on the specific case of 1 raised to any power. Regardless of the exponent, 1 raised to that power always equals 1. This is because multiplying 1 by itself any number of times results in 1.
Why is this the case?
This stems directly from the definition of exponents and the multiplicative identity property of 1. The multiplicative identity property states that any number multiplied by 1 remains unchanged. Therefore, 1<sup>5</sup> simply means 1 × 1 × 1 × 1 × 1, which equals 1.
Examples:
- 1¹ = 1
- 1² = 1 × 1 = 1
- 1³ = 1 × 1 × 1 = 1
- 1⁴ = 1 × 1 × 1 × 1 = 1
- 1⁵ = 1 × 1 × 1 × 1 × 1 = 1
- And so on...
This principle holds true for any positive integer exponent, any negative integer exponent (resulting in 1/1 which simplifies to 1), and even for zero exponents (defined as 1).
Applications of Exponents
Exponents are not just abstract mathematical concepts; they have practical applications in various fields:
1. Finance: Compound Interest
Compound interest calculations rely heavily on exponents. The formula for compound interest involves exponential growth, where the principal amount grows exponentially over time.
2. Science: Exponential Growth and Decay
Many natural phenomena exhibit exponential growth or decay. Population growth, radioactive decay, and the spread of diseases can be modeled using exponential functions.
3. Computer Science: Binary Numbers and Data Storage
Binary numbers, the foundation of computer systems, utilize exponents of 2 to represent data. Each bit in a binary number represents a power of 2.
4. Engineering: Calculating Areas and Volumes
Calculating the area of squares, cubes, and other geometric shapes often involves exponents. The formulas for these calculations frequently incorporate exponents to reflect the dimensionality of the shapes.
5. Physics: Describing Physical Phenomena
Exponents are essential in many physical laws and formulas, for instance, describing the intensity of light or the force of gravity.
Beyond the Basics: Exploring More Complex Exponents
While this article primarily focuses on positive integer exponents, it's important to acknowledge that exponents can be extended to include:
- Zero exponent: a⁰ = 1 (for any non-zero a).
- Negative exponents: a<sup>-n</sup> = 1/a<sup>n</sup>.
- Fractional exponents: a<sup>m/n</sup> = <sup>n</sup>√a<sup>m</sup> (the nth root of a raised to the mth power).
Understanding these extensions allows for the solving of more complex mathematical problems and expands the applicability of exponential functions.
Conclusion: The Significance of Simplicity
The seemingly trivial calculation of 1 raised to the 5th power underscores the fundamental importance of basic mathematical concepts. While the answer is simple, the underlying principles of exponents are far-reaching and essential to numerous fields. Understanding exponents lays the groundwork for more complex mathematical concepts and provides crucial tools for solving real-world problems in various disciplines. The simplicity of 1 to any power highlights the elegance and power of fundamental mathematical principles, reminding us that even the most basic concepts can have profound and widespread implications. This understanding allows for a deeper appreciation of mathematics and its role in shaping our understanding of the world around us.
Latest Posts
Latest Posts
-
What Is The Symbol For Entropy
Apr 03, 2025
-
6 Less Than The Product Of 4 And X
Apr 03, 2025
-
What Planet Is The Closest Size To Earth
Apr 03, 2025
-
How Many Fl Oz In A Fifth
Apr 03, 2025
-
List Two Radioactive Isotopes Of Oxygen
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 To The 5th Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
