Do All Parallelograms Have 4 Right Angles
listenit
Mar 31, 2025 · 5 min read
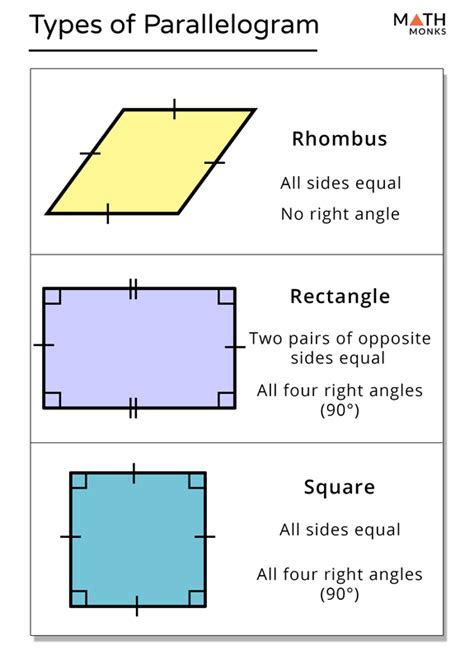
Table of Contents
Do All Parallelograms Have 4 Right Angles? Exploring Quadrilateral Properties
The simple answer is: no, not all parallelograms have four right angles. While parallelograms possess several key properties, the presence of four right angles is a defining characteristic of a specific type of parallelogram – the rectangle. This article will delve deeper into the properties of parallelograms and rectangles, clarifying the distinctions and exploring related geometric concepts. Understanding these differences is crucial for mastering geometry and tackling more complex problems.
Understanding Parallelograms: Key Properties
A parallelogram is a quadrilateral (a four-sided polygon) with specific properties that distinguish it from other quadrilaterals. These defining characteristics are:
- Opposite sides are parallel: This is the most fundamental property. The opposite sides of a parallelogram are parallel to each other. This parallelism is what gives the parallelogram its name.
- Opposite sides are equal in length: Not only are the opposite sides parallel, but they are also congruent (equal in length).
- Opposite angles are equal: The angles opposite each other within a parallelogram are equal in measure.
- Consecutive angles are supplementary: Any two angles that are next to each other (consecutive) add up to 180 degrees. This is a direct consequence of the parallel lines.
Let's visualize this with a diagram:
B
/ \
/ \
/ \
/_______\
A C
D
In parallelogram ABCD, AB is parallel to DC, and AD is parallel to BC. AB = DC and AD = BC. ∠A = ∠C and ∠B = ∠D. ∠A + ∠B = 180°, ∠B + ∠C = 180°, ∠C + ∠D = 180°, and ∠D + ∠A = 180°.
Rectangles: A Special Case of Parallelograms
A rectangle is a type of parallelogram that possesses an additional crucial property:
- All angles are right angles (90 degrees): This is the defining characteristic that separates a rectangle from other parallelograms. All four interior angles of a rectangle measure 90 degrees.
Because a rectangle is a parallelogram, it inherits all the properties of a parallelogram: opposite sides are parallel and equal, opposite angles are equal, and consecutive angles are supplementary. However, the presence of right angles adds a significant level of geometric constraint and opens up additional avenues for calculations and problem-solving.
Visualizing the Difference
Consider these two shapes:
Parallelogram (not a rectangle):
B
/ \
/ \
/ \
/_______\
A C
D
Here, angles A and C are equal, as are angles B and D. However, the angles are not 90 degrees.
Rectangle:
B
| |
| |
| |
A____|____C
D
In this case, all angles are 90 degrees. The sides are still parallel and equal in length (opposite sides), but the presence of right angles fundamentally changes the geometry.
Other Parallelograms: Rhombuses and Squares
Two other notable types of parallelograms are rhombuses and squares.
-
Rhombus: A rhombus is a parallelogram where all four sides are equal in length. However, its angles are not necessarily right angles.
-
Square: A square is a parallelogram with the most restrictive properties. It's both a rectangle (all angles are 90 degrees) and a rhombus (all sides are equal in length). Therefore, a square possesses all the properties of both rectangles and rhombuses.
This hierarchy is important to understand:
- Parallelogram: The most general category.
- Rectangle: A parallelogram with four right angles.
- Rhombus: A parallelogram with four equal sides.
- Square: A parallelogram that is both a rectangle and a rhombus (four right angles and four equal sides).
Proofs and Demonstrations
Let's explore a geometric proof demonstrating that a parallelogram with one right angle is a rectangle.
Theorem: If one angle of a parallelogram is a right angle, then the parallelogram is a rectangle.
Proof:
-
Given: Parallelogram ABCD with ∠A = 90°.
-
Opposite angles are equal: In parallelogram ABCD, ∠A = ∠C (opposite angles are equal). Therefore, ∠C = 90°.
-
Consecutive angles are supplementary: In parallelogram ABCD, ∠A + ∠B = 180° (consecutive angles are supplementary). Since ∠A = 90°, then ∠B = 180° - 90° = 90°.
-
Opposite angles are equal: ∠B = ∠D (opposite angles are equal). Therefore, ∠D = 90°.
-
Conclusion: Since all angles (∠A, ∠B, ∠C, ∠D) are 90°, parallelogram ABCD is a rectangle.
This proof highlights the strong relationship between the properties of parallelograms and the specific definition of a rectangle. The existence of just one right angle automatically forces all other angles to be right angles, thus transforming the parallelogram into a rectangle.
Real-World Applications
Understanding the differences between parallelograms and rectangles has significant real-world applications across various fields:
-
Architecture and Construction: Rectangles are frequently used in building design due to their stability and ease of construction. Parallelograms, while less common in structural applications, might appear in more artistic or design-oriented elements.
-
Engineering: Many engineering designs utilize parallelograms and rectangles for creating stable and predictable structures. The properties of these shapes are crucial for calculations related to stress, strain, and stability.
-
Graphic Design and Art: Parallelograms and rectangles are fundamental shapes in graphic design and art, influencing composition and visual balance.
-
Computer Graphics and Game Development: These shapes are fundamental building blocks in computer graphics, used to create objects, environments, and game elements.
Conclusion: Precision in Geometric Definitions
The key takeaway is that while all rectangles are parallelograms, not all parallelograms are rectangles. The presence of four right angles is a defining feature that distinguishes rectangles from the broader category of parallelograms. Understanding this distinction is critical for solving geometric problems, applying geometric principles to real-world situations, and mastering more advanced mathematical concepts. The subtle differences between these shapes underscore the importance of precise definitions and rigorous logical reasoning in mathematics. Mastering these foundational geometric concepts provides a solid base for tackling more advanced topics in geometry and related fields. Remember the hierarchy: squares are rectangles, rectangles are parallelograms, but not all parallelograms are rectangles or squares. This clarifies the specific properties that define each shape. Through careful analysis and proof, we can fully grasp the unique characteristics of each quadrilateral.
Latest Posts
Latest Posts
-
Number Of Valence Electrons In Silicon
Apr 01, 2025
-
What Is 2 9 In A Decimal
Apr 01, 2025
-
What Is 24 Divided By 4
Apr 01, 2025
-
Milk Turning Sour Is A Chemical Change
Apr 01, 2025
-
Where On The Periodic Table Are Metals Found
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Do All Parallelograms Have 4 Right Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
