Convert The Equation To Polar Form
listenit
Apr 04, 2025 · 5 min read
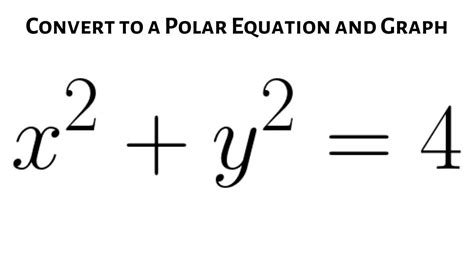
Table of Contents
Converting Equations to Polar Form: A Comprehensive Guide
Converting equations from rectangular (Cartesian) coordinates to polar coordinates, and vice versa, is a fundamental skill in mathematics, particularly useful in calculus, physics, and engineering. This comprehensive guide will walk you through the process, covering various types of equations and providing practical examples to solidify your understanding. We'll delve into the underlying principles and explore strategies for handling different scenarios effectively.
Understanding Rectangular and Polar Coordinate Systems
Before diving into conversions, let's refresh our understanding of the two coordinate systems.
Rectangular Coordinates (Cartesian Coordinates)
This system uses two perpendicular axes, the x-axis and the y-axis, to locate a point in a plane. A point is represented by an ordered pair (x, y), where x represents the horizontal distance from the origin and y represents the vertical distance.
Polar Coordinates
In the polar coordinate system, a point is defined by its distance from the origin (pole) and its angle from the positive x-axis. This distance is denoted by r (radius) and the angle by θ (theta). A point is represented by an ordered pair (r, θ).
The relationship between the two systems is key to the conversion process.
The Fundamental Conversion Formulas
The core of converting between rectangular and polar coordinates lies in these formulas:
-
From Rectangular to Polar:
r = √(x² + y²)θ = arctan(y/x)(Note: Consider the quadrant to determine the correct angle)
-
From Polar to Rectangular:
x = r cos(θ)y = r sin(θ)
These formulas are derived directly from trigonometric relationships within a right-angled triangle formed by the point, the origin, and the projections onto the x and y axes.
Converting Equations from Rectangular to Polar Form
Let's explore how to convert various types of equations from rectangular to polar form.
1. Equations Representing Circles
Example: Convert the equation of a circle x² + y² = 25 to polar form.
This is a straightforward conversion. Since r² = x² + y², we can directly substitute:
r² = 25
Therefore, the polar form is simply r = 5 (we only consider the positive root as r represents distance). This shows that the equation represents a circle with radius 5 centered at the origin.
2. Equations Representing Lines
Example: Convert the equation of a line y = x to polar form.
Substitute the rectangular-to-polar conversion formulas:
r sin(θ) = r cos(θ)
We can divide both sides by r (assuming r ≠ 0, which excludes the origin):
sin(θ) = cos(θ)
Dividing by cos(θ) (assuming cos(θ) ≠ 0):
tan(θ) = 1
Therefore, θ = π/4 or 45 degrees. This equation represents a line passing through the origin at a 45-degree angle.
Important Note: Handling lines that don't pass through the origin requires a more nuanced approach, often involving manipulating the equation to isolate either x or y before substituting.
3. Equations Representing Parabolas, Ellipses, and Hyperbolas
Converting conic sections (parabolas, ellipses, hyperbolas) to polar form usually involves more algebraic manipulation. Let's consider a general approach:
- Substitute: Replace x and y with their polar equivalents (
r cos(θ)andr sin(θ)). - Simplify: Use trigonometric identities and algebraic techniques to simplify the equation.
- Solve for r: Express the equation in a form where r is isolated as a function of θ.
Example (Ellipse): Convert the equation x² + 4y² = 4 to polar form.
- Substitute:
(r cos(θ))² + 4(r sin(θ))² = 4 - Simplify:
r²(cos²(θ) + 4sin²(θ)) = 4 - Solve for r:
r² = 4 / (cos²(θ) + 4sin²(θ))r = ± 2 / √(cos²(θ) + 4sin²(θ))
This illustrates how conic sections transform into more complex polar equations.
4. Equations Representing Other Curves
Many other types of curves can be converted. The process always remains the same: substitute and simplify. The complexity depends on the initial equation's form.
Converting Equations from Polar to Rectangular Form
The conversion from polar to rectangular form is generally more straightforward. We directly substitute the formulas for x and y.
Example: Convert the polar equation r = 2cos(θ) to rectangular form.
- Multiply by r:
r² = 2r cos(θ)(This step is often crucial) - Substitute:
x² + y² = 2x - Rearrange:
x² - 2x + y² = 0 - Complete the square:
(x - 1)² + y² = 1
This shows that the polar equation r = 2cos(θ) represents a circle with radius 1 centered at (1,0).
Advanced Techniques and Considerations
- Dealing with Undefined Values: Be mindful of situations where
r = 0orcos(θ) = 0orsin(θ) = 0. These cases require separate consideration to avoid division by zero. - Trigonometric Identities: Mastering trigonometric identities is crucial for simplifying the resulting equations.
- Multiple Representations: A single point in the plane can be represented by multiple polar coordinates (e.g., (r, θ) and (-r, θ + π)).
- Software Tools: Mathematical software (like Mathematica, Maple, or MATLAB) can be incredibly helpful for verifying results and handling complex conversions.
Practical Applications
The ability to convert between rectangular and polar coordinates is vital in many fields:
- Physics: Analyzing projectile motion, analyzing circular motion, and representing forces in two dimensions.
- Engineering: Designing circular structures, analyzing antenna radiation patterns, and creating graphical representations of data in polar plots.
- Calculus: Evaluating double integrals over circular regions and calculating areas and volumes.
- Computer Graphics: Creating curves and shapes in polar coordinates for computer-aided design (CAD) applications.
Conclusion
Converting equations between rectangular and polar forms is a crucial skill that requires a firm grasp of the fundamental conversion formulas and a proficiency in algebraic manipulation and trigonometric identities. By understanding the underlying principles and following a systematic approach, you can confidently tackle conversions of various complexities, unlocking insights into the geometric properties of equations and expanding your problem-solving capabilities across diverse fields. Remember to practice regularly with different types of equations to build your competence and confidence in this essential mathematical technique.
Latest Posts
Latest Posts
-
Is 7 3 A Rational Number
Apr 04, 2025
-
How Do You Find Ml Quantum Number
Apr 04, 2025
-
How Many Unpaired Electrons Does Manganese Have
Apr 04, 2025
-
Water Is Made Up Of Which Two Elements
Apr 04, 2025
-
What Is 9 Percent Of 50
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Convert The Equation To Polar Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
