Is 7 3 A Rational Number
listenit
Apr 04, 2025 · 5 min read
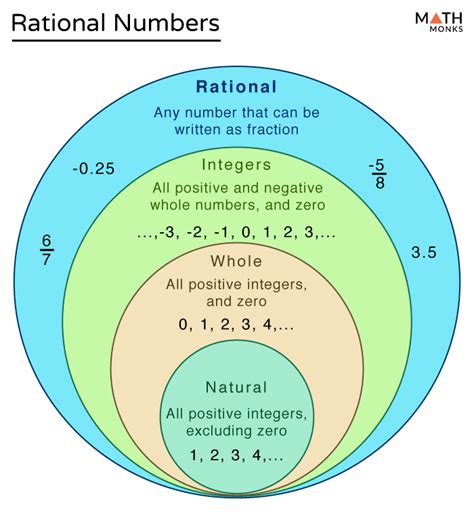
Table of Contents
Is 7/3 a Rational Number? A Deep Dive into Rational and Irrational Numbers
The question, "Is 7/3 a rational number?" might seem simple at first glance. However, understanding the answer requires a firm grasp of the definitions of rational and irrational numbers. This article will not only answer the question definitively but also delve into the broader concepts of rational and irrational numbers, exploring their properties, examples, and significance in mathematics. We'll also touch upon how to identify rational numbers and dispel common misconceptions.
Understanding Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p is the numerator and q is the non-zero denominator. The key here is that both the numerator and the denominator must be integers (whole numbers, including zero, but the denominator cannot be zero). Integers include positive whole numbers, negative whole numbers, and zero.
Examples of Rational Numbers:
- 1/2: One-half is a classic example. Both 1 and 2 are integers.
- -3/4: Negative three-quarters is also rational; -3 and 4 are integers.
- 5: The integer 5 can be expressed as 5/1, fulfilling the definition.
- 0: Zero can be expressed as 0/1, making it a rational number.
- 0.75: This decimal can be expressed as the fraction 3/4, which satisfies the definition.
- -2.25: This decimal can be expressed as -9/4, making it a rational number.
Key characteristics of rational numbers:
- They can be expressed as fractions: This is the defining characteristic.
- Their decimal representations either terminate or repeat: For example, 1/4 is 0.25 (terminating), while 1/3 is 0.333... (repeating).
- They are countable: This means that, theoretically, you could list all rational numbers. This is a significant difference from irrational numbers.
Understanding Irrational Numbers
In contrast to rational numbers, irrational numbers cannot be expressed as a simple fraction of two integers. Their decimal representations are non-terminating and non-repeating. This means they go on forever without ever establishing a repeating pattern.
Examples of Irrational Numbers:
- π (pi): The ratio of a circle's circumference to its diameter, approximately 3.14159..., is famous for its infinite, non-repeating decimal expansion.
- √2 (the square root of 2): This number cannot be expressed as a fraction of two integers. Its decimal representation is approximately 1.41421356..., continuing infinitely without repeating.
- e (Euler's number): The base of the natural logarithm, approximately 2.71828..., is another well-known irrational number.
- √5 (the square root of 5): Similar to √2, this number cannot be expressed as a simple fraction.
- φ (the golden ratio): Approximately 1.61803..., it's an irrational number with significant appearances in nature and art.
Key characteristics of irrational numbers:
- They cannot be expressed as fractions of integers: This is the defining characteristic.
- Their decimal representations are non-terminating and non-repeating: They go on forever without repeating patterns.
- They are uncountable: This signifies that you cannot create a list of all irrational numbers.
Back to the Main Question: Is 7/3 a Rational Number?
Now, let's return to the original question. Is 7/3 a rational number? The answer is a resounding yes.
Why?
Because 7 and 3 are both integers, and 7/3 fits perfectly into the definition of a rational number. It can be expressed as a fraction of two integers. Its decimal representation is 2.333..., which is a repeating decimal, another characteristic of rational numbers.
Identifying Rational Numbers: A Practical Guide
Identifying whether a number is rational often involves these steps:
-
Check if it's an integer: If it is, it's automatically rational (as it can be expressed as itself over 1).
-
Check if it's a terminating decimal: If the decimal representation ends, it's rational. You can often convert it to a fraction by considering the place value of the last digit. For example, 0.25 is 25/100, which simplifies to 1/4.
-
Check if it's a repeating decimal: If the decimal representation has a repeating pattern, it's rational. Converting repeating decimals to fractions requires a specific method, but it's always possible. For example, 0.333... is equal to 1/3.
-
Check if it's a simple fraction: If the number is already expressed as a fraction, check if both numerator and denominator are integers. If they are, and the denominator is not zero, it's rational.
-
Consider square roots: Be cautious with square roots. The square roots of perfect squares (like √4 = 2, √9 = 3) are rational. However, the square roots of non-perfect squares (like √2, √3, √5) are irrational.
Dispelling Common Misconceptions about Rational Numbers
Several misconceptions often surround rational numbers. Let's address a few:
-
Misconception 1: All decimals are irrational. This is incorrect. Terminating and repeating decimals are rational. Only non-terminating, non-repeating decimals are irrational.
-
Misconception 2: Large numbers are always irrational. Size has no bearing on whether a number is rational or irrational. A huge number like 1,000,000 is rational (it's 1,000,000/1).
-
Misconception 3: Rational numbers are only simple fractions. While simple fractions are a subset of rational numbers, any number expressible as a fraction of two integers (even complex ones) is rational.
The Significance of Rational and Irrational Numbers
The distinction between rational and irrational numbers is fundamental in mathematics. Many mathematical concepts and theorems rely on this classification. Understanding the difference is crucial for various branches of mathematics, including:
- Calculus: Understanding limits and continuity heavily relies on the concept of rational and irrational numbers.
- Number Theory: This branch of mathematics extensively deals with properties of both rational and irrational numbers.
- Geometry: The relationship between rational and irrational numbers is often demonstrated geometrically (e.g., constructing a square root of 2).
- Algebra: Solving equations and inequalities often involves working with both rational and irrational numbers.
Conclusion: 7/3 is Definitely Rational
In conclusion, 7/3 is indeed a rational number. It satisfies all the criteria of a rational number: it's expressible as a fraction of two integers, and its decimal representation is a repeating decimal. Understanding the definitions and characteristics of rational and irrational numbers is crucial for a strong foundation in mathematics. This knowledge will help you solve problems, analyze mathematical concepts, and appreciate the beauty and complexity of the number system. Remember the key differences: rational numbers can be expressed as fractions of integers; irrational numbers cannot. Using this understanding, you can confidently identify whether any number is rational or irrational.
Latest Posts
Latest Posts
-
How Many Tenths Are In A Foot
Apr 05, 2025
-
Write 9 50 As A Decimal Number
Apr 05, 2025
-
What Is 1 4 1 5
Apr 05, 2025
-
Determine Whether The Quantitative Variable Is Discrete Or Continuous
Apr 05, 2025
-
How Does Atomic Radius Increase Across The Periodic Table
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Is 7 3 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
