Common Factors Of 4 And 10
listenit
Apr 05, 2025 · 5 min read
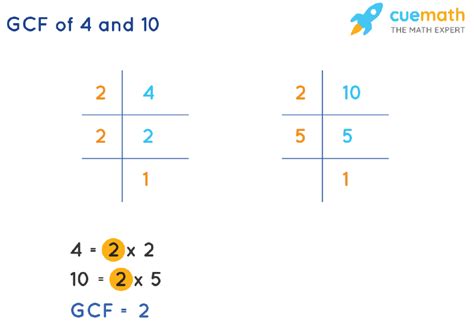
Table of Contents
Unveiling the Secrets: A Deep Dive into the Common Factors of 4 and 10
Finding the common factors of two numbers might seem like a simple arithmetic task, but delving deeper reveals fascinating connections to number theory and its broader applications. This article explores the common factors of 4 and 10, providing a comprehensive understanding not only of the solution but also the underlying mathematical principles involved. We'll move beyond the basic answer to uncover the rich tapestry of concepts related to factors, divisibility, and the fundamental theorem of arithmetic.
Understanding Factors and Divisibility
Before we delve into the specifics of 4 and 10, let's establish a firm foundation. A factor (or divisor) of a number is a whole number that divides evenly into that number without leaving a remainder. For example, the factors of 6 are 1, 2, 3, and 6 because 6 ÷ 1 = 6, 6 ÷ 2 = 3, 6 ÷ 3 = 2, and 6 ÷ 6 = 1. Divisibility is the property of one number being completely divisible by another. Understanding divisibility rules is crucial for efficient factor identification.
Divisibility Rules: A Quick Refresher
Knowing divisibility rules significantly speeds up the process of finding factors. Some key rules include:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
- Divisibility by 4: A number is divisible by 4 if the number formed by its last two digits is divisible by 4.
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.
- Divisibility by 10: A number is divisible by 10 if its last digit is 0.
Finding the Factors of 4 and 10
Now, let's apply this knowledge to our target numbers: 4 and 10.
Factors of 4:
Using the divisibility rules, we can quickly identify the factors of 4:
- 1: 4 ÷ 1 = 4
- 2: 4 ÷ 2 = 2
- 4: 4 ÷ 4 = 1
Therefore, the factors of 4 are 1, 2, and 4.
Factors of 10:
Similarly, let's find the factors of 10:
- 1: 10 ÷ 1 = 10
- 2: 10 ÷ 2 = 5
- 5: 10 ÷ 5 = 2
- 10: 10 ÷ 10 = 1
Thus, the factors of 10 are 1, 2, 5, and 10.
Identifying Common Factors
The common factors of 4 and 10 are the numbers that appear in both lists of factors. Comparing the factors of 4 (1, 2, 4) and the factors of 10 (1, 2, 5, 10), we see that 1 and 2 are present in both sets.
Therefore, the common factors of 4 and 10 are 1 and 2.
Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the highest common factor (HCF), is the largest number that divides both numbers without leaving a remainder. In our case, the GCF of 4 and 10 is 2. Understanding the GCF is crucial in various mathematical operations, including simplifying fractions and solving algebraic equations.
Prime Factorization: A Deeper Look
Prime factorization is a powerful technique for finding the GCF and understanding the fundamental building blocks of numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. The fundamental theorem of arithmetic states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
Let's perform prime factorization for 4 and 10:
- 4 = 2 x 2 = 2² (4 is composed of two prime factors, both 2)
- 10 = 2 x 5 (10 is composed of two distinct prime factors, 2 and 5)
By examining the prime factorizations, we can easily identify the common prime factor: 2. The GCF is the product of the common prime factors raised to the lowest power. In this instance, the GCF is 2¹ = 2. This method provides a more systematic approach, especially when dealing with larger numbers.
Applications of Common Factors and GCF
The concepts of common factors and the greatest common factor have widespread applications beyond simple arithmetic. Here are a few examples:
-
Simplifying Fractions: Finding the GCF allows us to simplify fractions to their lowest terms. For instance, the fraction 4/10 can be simplified to 2/5 by dividing both the numerator and denominator by their GCF (2).
-
Algebraic Simplification: The GCF plays a vital role in simplifying algebraic expressions. Factoring out the GCF helps to reduce the complexity of equations and makes them easier to solve.
-
Geometry and Measurement: GCF is used in solving geometric problems involving areas and lengths. For example, when determining the largest square tile that can perfectly cover a rectangular floor, the GCF of the floor's dimensions is crucial.
-
Cryptography: Prime factorization is fundamental to many cryptographic systems, including the widely used RSA algorithm, which relies on the difficulty of factoring large numbers into their prime components.
Exploring Further: Least Common Multiple (LCM)
While we've focused on common factors, it's worth mentioning the least common multiple (LCM). The LCM is the smallest number that is a multiple of both numbers. Finding the LCM is equally important in various applications, such as adding and subtracting fractions with different denominators. To find the LCM of 4 and 10, we can use the prime factorization method or list multiples:
Multiples of 4: 4, 8, 12, 16, 20, 24... Multiples of 10: 10, 20, 30, 40...
The smallest common multiple is 20.
The relationship between the GCF and LCM is given by the formula: GCF(a, b) * LCM(a, b) = a * b. In our example: 2 * 20 = 4 * 10 = 40. This formula provides a useful shortcut for finding the LCM if the GCF is already known.
Conclusion: Beyond the Basics of Common Factors
Determining the common factors of 4 and 10, while seemingly straightforward, opens a door to a vast world of mathematical concepts. From divisibility rules and prime factorization to the fundamental theorem of arithmetic and their applications in various fields, understanding factors provides a robust foundation for advanced mathematical studies and problem-solving. This article has served as an introduction to these concepts, encouraging further exploration and a deeper appreciation for the interconnectedness of seemingly simple mathematical ideas. The ability to identify common factors, calculate GCF and LCM is a fundamental skill applicable across various mathematical disciplines and real-world applications. Mastering these concepts sets the stage for more advanced mathematical explorations and problem-solving capabilities.
Latest Posts
Latest Posts
-
How Many Protons Electrons And Neutrons Does Sulfur Have
Apr 05, 2025
-
Is Hydrogen Metal Nonmetal Or Metalloid
Apr 05, 2025
-
What Is The Prime Factorization Of 196
Apr 05, 2025
-
The Surface Of A Mirror Is Flat
Apr 05, 2025
-
Common Factors Of 8 And 24
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Common Factors Of 4 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
