Area Of A Circle With A Radius Of 7
listenit
Apr 03, 2025 · 5 min read
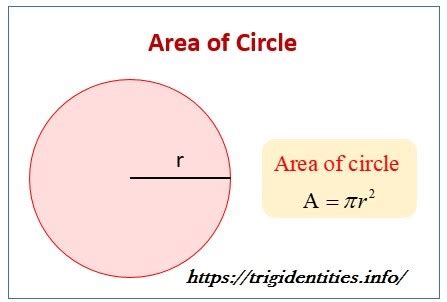
Table of Contents
Calculating the Area of a Circle with a Radius of 7: A Comprehensive Guide
Determining the area of a circle is a fundamental concept in geometry with widespread applications in various fields, from engineering and architecture to data science and beyond. This comprehensive guide will delve into the calculation of the area of a circle with a radius of 7 units, exploring the formula, the mathematical process, and practical examples. We'll also touch upon related concepts and potential applications.
Understanding the Formula: πr²
The area of a circle is calculated using a simple yet elegant formula: Area = πr², where:
- A represents the area of the circle.
- π (pi) is a mathematical constant, approximately equal to 3.14159. It represents the ratio of a circle's circumference to its diameter.
- r represents the radius of the circle, which is the distance from the center of the circle to any point on its circumference.
This formula encapsulates the relationship between a circle's radius and its area. The square of the radius signifies that the area increases quadratically with the radius; doubling the radius quadruples the area.
Calculating the Area with a Radius of 7
Let's apply the formula to calculate the area of a circle with a radius of 7 units. We'll substitute 'r' with 7 in the formula:
Area = π * 7²
Area = π * 49
Now, we need to approximate the value of π. While π is an irrational number (meaning its decimal representation goes on forever without repeating), we can use a commonly accepted approximation, such as 3.14159 or simply 3.14. The more decimal places you use, the more accurate your result will be.
Using π ≈ 3.14159:
Area ≈ 3.14159 * 49 ≈ 153.938 square units
Using π ≈ 3.14:
Area ≈ 3.14 * 49 ≈ 153.86 square units
As you can see, the difference between the two approximations is relatively small, but the more precise value of π provides a more accurate result. For most practical purposes, 3.14 is a sufficient approximation.
Practical Applications and Real-World Examples
The ability to calculate the area of a circle has countless applications across various disciplines. Here are a few examples:
1. Engineering and Construction:
- Determining the amount of material needed: Imagine you need to build a circular swimming pool with a radius of 7 meters. Calculating the area will help determine the quantity of concrete, tiles, or other materials required.
- Designing circular structures: Architects and engineers use the area calculation to optimize the design of circular structures such as stadiums, water tanks, or ventilation systems.
2. Agriculture and Forestry:
- Irrigation systems: Calculating the area of a circular irrigation field helps determine the water needed for efficient crop management.
- Forestry management: Estimating the area of a circular forest plot helps in resource assessment and management planning.
3. Data Science and Statistics:
- Data visualization: Circular charts and graphs, such as pie charts, utilize the concept of area to represent proportions of data visually. Understanding how area relates to radius is crucial for creating accurate and informative visualizations.
- Probability and statistics: Certain statistical distributions involve circular areas, making area calculations essential for data analysis.
4. Everyday Life:
- Pizza size: The area of a pizza is directly related to the amount of pizza you get. Knowing the radius allows you to compare different pizza sizes.
- Circular gardens or flower beds: Similar to the pool example, determining the area of a circular garden helps in planning its design and the resources needed for maintenance.
Exploring Related Concepts
Understanding the area of a circle opens the door to exploring related concepts in geometry:
1. Circumference of a Circle:
The circumference (perimeter) of a circle is calculated using the formula: Circumference = 2πr. Knowing the radius (7 units in our case), we can easily calculate the circumference:
Circumference ≈ 2 * 3.14159 * 7 ≈ 43.98 units
This is crucial for applications involving the length of the boundary of a circular region.
2. Area of a Sector:
A sector is a portion of a circle enclosed between two radii and an arc. The area of a sector is calculated as: Area of sector = (θ/360°) * πr², where θ is the central angle of the sector in degrees.
3. Area of a Segment:
A segment is the area between a chord and an arc of a circle. Calculating the area of a segment requires more complex calculations involving trigonometry.
4. Relationship between Area and Diameter:
Since the diameter (d) is twice the radius (d = 2r), the area formula can also be written as: Area = π(d/2)² = (πd²)/4. This alternative formula is useful when the diameter is known instead of the radius.
Beyond the Basics: Advanced Applications
The fundamental understanding of calculating the area of a circle serves as a foundation for more advanced geometrical concepts and applications:
- Calculus: The concept of area is crucial in integral calculus, where the area under a curve is calculated using integration.
- Three-dimensional geometry: The area of a circle is fundamental in calculating the surface area and volume of three-dimensional shapes like cylinders, cones, and spheres.
- Coordinate Geometry: Circles can be represented by equations, and understanding the area allows for manipulation and analysis of these equations.
Conclusion: Mastering Circle Area Calculations
Calculating the area of a circle with a radius of 7, or any radius for that matter, is a fundamental skill with far-reaching implications across numerous fields. The seemingly simple formula, πr², represents a powerful tool for solving practical problems and understanding complex mathematical concepts. By understanding the formula, its applications, and related geometrical concepts, you equip yourself with a valuable skillset that extends beyond the classroom and into the real world. Remember to utilize the appropriate level of precision for π based on the required accuracy of your calculations. With practice, you'll master the art of calculating circle areas and apply this knowledge to a wide range of situations.
Latest Posts
Latest Posts
-
What Is Molar Volume Of Gas At Stp
Apr 04, 2025
-
Man Is The Only Animal That Blushes Or Needs To
Apr 04, 2025
-
In What Organelle Does Cellular Respiration Occur In
Apr 04, 2025
-
How Many Electrons Are In Bromine
Apr 04, 2025
-
Which Organelle Does Cellular Respiration Occur In
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Area Of A Circle With A Radius Of 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
