An Equilateral Triangle Is An Isosceles Triangle
listenit
Mar 27, 2025 · 5 min read
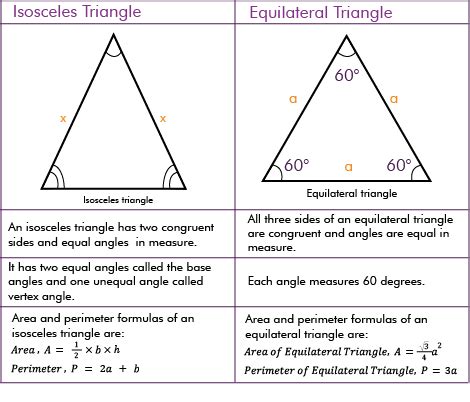
Table of Contents
An Equilateral Triangle Is an Isosceles Triangle: A Deep Dive into Geometric Definitions
The statement "an equilateral triangle is an isosceles triangle" is a fundamental truth in geometry, yet its implications and underlying logic often warrant a deeper exploration. This article will not only prove this assertion rigorously but also delve into the definitions of both equilateral and isosceles triangles, examine the relationships between different types of triangles, and explore the broader significance of this seemingly simple geometric fact.
Defining the Key Terms: Isosceles and Equilateral Triangles
Before we can demonstrate the relationship between equilateral and isosceles triangles, we must clearly define each term:
Isosceles Triangle Definition
An isosceles triangle is a triangle with at least two sides of equal length. These equal sides are called legs, and the angle between them is called the vertex angle. The side opposite the vertex angle is called the base. It's crucial to note the "at least two" part of the definition. This means that all equilateral triangles are also isosceles triangles, as they fulfill the condition of having at least two equal sides. However, not all isosceles triangles are equilateral.
Equilateral Triangle Definition
An equilateral triangle is a triangle with all three sides of equal length. Consequently, all three angles are also equal, each measuring 60 degrees. This inherent symmetry makes equilateral triangles highly significant in various mathematical and scientific fields.
Proving the Assertion: An Equilateral Triangle is an Isosceles Triangle
The proof is straightforward and stems directly from the definitions:
-
Definition of an Equilateral Triangle: An equilateral triangle has three sides of equal length (let's denote these lengths as a, a, and a).
-
Definition of an Isosceles Triangle: An isosceles triangle has at least two sides of equal length.
-
Comparison: Since an equilateral triangle possesses three sides of equal length (a, a, a), it automatically satisfies the condition of having at least two sides of equal length.
-
Conclusion: Therefore, an equilateral triangle is an isosceles triangle. This is a deductive argument; the conclusion logically follows from the premises (the definitions).
This proof highlights a crucial concept in mathematical logic: set inclusion. The set of equilateral triangles is a subset of the set of isosceles triangles. All equilateral triangles belong to the larger category of isosceles triangles, but not all isosceles triangles are equilateral.
Visualizing the Relationship: Venn Diagrams and Geometric Representations
A Venn diagram provides a clear visual representation of this relationship. Draw two overlapping circles. Label one circle "Isosceles Triangles" and the other "Equilateral Triangles." The circle representing equilateral triangles should be entirely contained within the circle representing isosceles triangles. This visually demonstrates that every equilateral triangle is also an isosceles triangle, but not vice versa.
Exploring the Converse: Is an Isosceles Triangle an Equilateral Triangle?
The converse of the statement "an equilateral triangle is an isosceles triangle" is false. An isosceles triangle does not necessarily have three equal sides. Many isosceles triangles exist with only two equal sides. Consider a triangle with sides of length 5, 5, and 7. This is an isosceles triangle because it has two sides of equal length (5 and 5), but it is not an equilateral triangle because all three sides are not equal.
This distinction emphasizes the importance of precise mathematical definitions and the need for careful logical reasoning. While a subset relationship exists between equilateral and isosceles triangles, the relationship is not reciprocal.
The Significance of Equilateral and Isosceles Triangles in Geometry
Both equilateral and isosceles triangles hold significant importance in various geometric contexts:
Equilateral Triangles: The Foundation of Regular Polygons
Equilateral triangles are the foundational building blocks of regular polygons. They are the simplest regular polygons, and their properties are used to derive properties of more complex shapes. They also play a crucial role in tessellations, where identical shapes fit together without gaps or overlaps.
Isosceles Triangles: Properties and Applications
Isosceles triangles possess several unique properties, including:
- Equal Base Angles: The two angles opposite the equal sides are also equal. This property is frequently used in geometric proofs and constructions.
- Altitude Bisects the Vertex Angle: The altitude from the vertex angle to the base bisects both the vertex angle and the base.
- Applications in Construction and Design: Isosceles triangles appear in many architectural and engineering designs due to their symmetry and structural stability.
Beyond the Basics: Exploring Advanced Concepts
The relationship between equilateral and isosceles triangles provides a springboard for exploring more advanced geometrical concepts:
Triangle Inequality Theorem:
This theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. This theorem helps to determine the possibility of constructing triangles with given side lengths. For isosceles and equilateral triangles, this theorem provides constraints on the lengths of the sides, ensuring that the triangle can be constructed.
Congruence and Similarity:
Equilateral triangles are highly congruent – meaning they have the same size and shape – if their side lengths are the same. Similarly, isosceles triangles with the same side length ratios are similar, meaning they have the same shape but different sizes. These concepts are fundamental to understanding geometric transformations and relationships.
Trigonometry and the Equilateral Triangle:
The equilateral triangle is fundamental in trigonometry. Its 60-degree angles serve as a basis for deriving trigonometric ratios for other angles.
Conclusion: Understanding the Nuances of Geometric Definitions
The seemingly simple statement "an equilateral triangle is an isosceles triangle" provides a valuable lesson in the precision of mathematical definitions and logical reasoning. By understanding the nuances of these definitions and their implications, we can appreciate the interconnectedness of various geometric concepts and their practical applications in diverse fields. The exploration of this relationship serves as a strong foundation for more advanced geometric studies and emphasizes the beauty and logic inherent in mathematics. This understanding allows for a more profound grasp of the underlying principles that govern geometric shapes and their interactions. Furthermore, appreciating the subtle differences and relationships between seemingly simple geometric objects like isosceles and equilateral triangles fosters a deeper understanding of mathematical rigor and precision.
Latest Posts
Latest Posts
-
How Many Electrons Can The S Sublevel Hold
Mar 30, 2025
-
How Much Of The World Is Desert
Mar 30, 2025
-
Cos X 1 X
Mar 30, 2025
-
What Is The Formula For Copper I Sulfide
Mar 30, 2025
-
1 2 Gallon Is How Many Cups
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about An Equilateral Triangle Is An Isosceles Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
