Cos X - 1 / X
listenit
Mar 30, 2025 · 5 min read
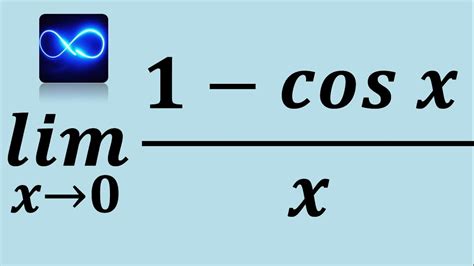
Table of Contents
Exploring the Function: (cos x - 1) / x
The function f(x) = (cos x - 1) / x presents a fascinating case study in mathematical analysis, combining trigonometric and algebraic elements that lead to interesting behaviors and applications. This article delves into a comprehensive exploration of this function, examining its properties, limits, series expansions, and potential applications. We'll unravel its intricacies and discover why it holds significance in various mathematical contexts.
Understanding the Function's Behavior
At first glance, the function f(x) = (cos x - 1) / x appears straightforward. However, its seemingly simple structure conceals subtle complexities. Let's begin by analyzing its behavior around key points:
The Point x = 0:
The function is undefined at x = 0 because division by zero is undefined. This singularity necessitates a careful examination of the function's behavior as x approaches 0. We can use L'Hôpital's rule or Taylor series expansions to investigate this limit. Using L'Hôpital's rule, we take the derivative of the numerator and denominator:
- Numerator: d(cos x - 1)/dx = -sin x
- Denominator: d(x)/dx = 1
Therefore, the limit as x approaches 0 is:
lim (x→0) (-sin x) / 1 = -sin(0) = 0
This tells us that while the function is undefined at x = 0, its limit as x approaches 0 is 0. This is a crucial observation that informs our understanding of the function's overall behavior.
Behavior for Large x:
As x becomes very large (positive or negative), the cosine function oscillates between -1 and 1. Consequently, the numerator (cos x - 1) oscillates between -2 and 0. The denominator, x, continues to grow in magnitude. Therefore, the function approaches 0 as x approaches ±∞. This asymptotic behavior is another important characteristic.
Taylor Series Expansion and Approximations
One powerful tool for analyzing this function is its Taylor series expansion around x = 0. Recall the Taylor series expansion for cos x:
cos x = 1 - x²/2! + x⁴/4! - x⁶/6! + ...
Substituting this into our function, we get:
(cos x - 1) / x = (1 - x²/2! + x⁴/4! - x⁶/6! + ... - 1) / x
Simplifying, we obtain:
(cos x - 1) / x = -x/2! + x³/4! - x⁵/6! + ...
This series expansion is particularly useful near x = 0. It provides a way to approximate the function's value for small x and also clarifies why the limit as x approaches 0 is 0. The first term dominates the behavior near 0, and as x approaches 0, this term also approaches 0.
Graphing the Function
Graphing the function f(x) = (cos x - 1) / x provides a visual representation of its behavior. The graph will show a smooth curve that approaches 0 as x approaches both 0 and ±∞. The curve will oscillate around the x-axis, reflecting the oscillatory nature of the cosine function in the numerator. The oscillations will dampen as |x| increases, reflecting the asymptotic behavior previously discussed. Observing the graph will reinforce our understanding of the function's key features.
Applications and Significance
While seemingly abstract, the function f(x) = (cos x - 1) / x finds applications in various mathematical and scientific fields:
Calculus and Limits:
The function serves as an excellent example for illustrating concepts such as limits, L'Hôpital's rule, and Taylor series expansions. Its analysis provides valuable practice in applying these fundamental calculus techniques.
Fourier Analysis:
The function, or variations thereof, may appear in Fourier analysis, which involves decomposing periodic functions into simpler trigonometric components. Understanding the function's behavior is relevant to interpreting such analyses.
Numerical Analysis:
Approximation techniques, including Taylor series expansions, play a crucial role in numerical analysis. The Taylor series expansion derived earlier for our function allows for accurate approximations within a certain radius of convergence, making it relevant to numerical computations.
Physics and Engineering:
Functions similar to (cos x - 1) / x, which represent damped oscillations or wave interference, can arise in the modeling of physical phenomena. The function's characteristics contribute to understanding the behavior of such systems.
Further Investigations and Extensions
Further explorations of this function could involve:
- Analyzing the derivative and second derivative: Examining the function's derivative and second derivative helps determine the function's monotonicity (increasing or decreasing intervals) and concavity (curvature).
- Investigating integrals involving the function: Determining the definite or indefinite integrals of the function can lead to interesting results and connections to other special functions.
- Exploring generalizations: Consider generalizations of the function, replacing cos x with other trigonometric functions or even more general periodic functions. This opens up a wider range of mathematical investigation.
- Numerical methods for evaluating the function: Developing efficient and accurate numerical methods for computing the value of the function for various inputs can be a practical application.
Conclusion
The seemingly simple function f(x) = (cos x - 1) / x reveals rich mathematical properties and connections to various mathematical branches. Through careful analysis using tools like L'Hôpital's rule, Taylor series expansions, and graphical representation, we've uncovered its key features: its behavior near x = 0, its asymptotic behavior for large x, and its potential applications in calculus, Fourier analysis, numerical analysis, and even physics and engineering. This exploration highlights the beauty and depth that can be found even in seemingly straightforward mathematical expressions. The function serves as a reminder of the importance of meticulous analysis and the power of combining different mathematical techniques to gain a deep understanding of mathematical objects. Further investigation into its properties and extensions will undoubtedly unveil even more fascinating aspects of this intriguing function.
Latest Posts
Latest Posts
-
How Many Membranes Surround A Chloroplast
Apr 01, 2025
-
Find Unit Vector Orthogonal To Two Vectors
Apr 01, 2025
-
A Substance That Is Dissolved In A Solution
Apr 01, 2025
-
How Are Electromagnetic Waves Different From Other Waves
Apr 01, 2025
-
What Part Of The Cow Does T Bone Come From
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Cos X - 1 / X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
