2x 3y 12 In Slope Intercept Form
listenit
Apr 02, 2025 · 6 min read
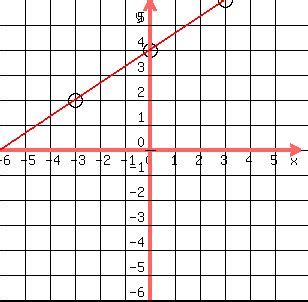
Table of Contents
Converting 2x + 3y = 12 to Slope-Intercept Form: A Comprehensive Guide
The equation 2x + 3y = 12 represents a straight line. While useful in its current form, converting it to slope-intercept form (y = mx + b) offers significant advantages in understanding its properties, such as its slope and y-intercept. This comprehensive guide will walk you through the conversion process step-by-step, explain the significance of the slope and y-intercept, and explore how this form aids in graphing and problem-solving.
Understanding Slope-Intercept Form (y = mx + b)
Before we dive into the conversion, let's refresh our understanding of the slope-intercept form of a linear equation: y = mx + b.
- y: Represents the dependent variable, typically plotted on the vertical axis.
- x: Represents the independent variable, typically plotted on the horizontal axis.
- m: Represents the slope of the line. The slope indicates the steepness and direction of the line. A positive slope indicates an upward trend from left to right, while a negative slope indicates a downward trend. The slope is calculated as the change in y divided by the change in x (rise over run).
- b: Represents the y-intercept, which is the point where the line intersects the y-axis (where x = 0).
Converting 2x + 3y = 12 to Slope-Intercept Form
The goal is to isolate y on one side of the equation. Here's how we do it:
-
Subtract 2x from both sides:
This step removes the x term from the left side, leaving only the y term:
3y = -2x + 12
-
Divide both sides by 3:
This isolates y, giving us the slope-intercept form:
y = (-2/3)x + 4
Therefore, the slope-intercept form of the equation 2x + 3y = 12 is y = (-2/3)x + 4.
Interpreting the Slope and Y-Intercept
Now that we have the equation in slope-intercept form, we can easily identify the slope and y-intercept:
-
Slope (m) = -2/3: This tells us that for every 3 units we move to the right along the x-axis, the line moves down 2 units along the y-axis. The negative sign indicates a downward slope.
-
Y-intercept (b) = 4: This means the line crosses the y-axis at the point (0, 4).
Graphing the Line
With the slope and y-intercept, graphing the line is straightforward:
-
Plot the y-intercept: Start by plotting the point (0, 4) on the y-axis.
-
Use the slope to find another point: From the y-intercept, use the slope (-2/3) to find another point on the line. Since the slope is -2/3, move 3 units to the right and 2 units down. This brings us to the point (3, 2).
-
Draw the line: Draw a straight line passing through the points (0, 4) and (3, 2). This line represents the equation 2x + 3y = 12.
Applications and Advantages of Slope-Intercept Form
The slope-intercept form offers several advantages:
-
Easy Identification of Slope and Y-intercept: As we've seen, the slope and y-intercept are immediately apparent. This simplifies calculations and interpretations.
-
Simple Graphing: The form facilitates easy graphing, as demonstrated above.
-
Predictive Power: The slope allows us to predict the value of y for any given value of x, and vice-versa. For instance, if x = 6, we can substitute this value into the equation: y = (-2/3)(6) + 4 = 0. Therefore, the point (6,0) lies on the line.
-
Problem Solving: The slope-intercept form is crucial in various applications, including:
-
Modeling real-world phenomena: Linear equations can model relationships between variables in various fields like physics, economics, and engineering. The slope-intercept form makes analyzing these relationships easier.
-
Finding intersections: When dealing with multiple lines, the slope-intercept form helps determine the point of intersection by solving a system of equations.
-
Determining parallel and perpendicular lines: Two lines are parallel if they have the same slope, and perpendicular if the product of their slopes is -1. The slope-intercept form makes these comparisons straightforward.
-
Further Exploration: Alternative Forms and Transformations
While the slope-intercept form is widely used, other forms of linear equations exist, each with its own advantages:
-
Standard Form (Ax + By = C): This form is useful when dealing with systems of equations and is easily convertible to slope-intercept form.
-
Point-Slope Form (y - y1 = m(x - x1)): This form is particularly useful when you know the slope and a point on the line.
It's important to be comfortable transforming between these forms, as this enhances your understanding of linear equations and their applications.
Advanced Applications and Problem Solving Examples
Let’s delve into some more complex scenarios involving the equation y = (-2/3)x + 4:
Example 1: Finding the x-intercept
The x-intercept is the point where the line crosses the x-axis (where y = 0). To find it, we set y = 0 in the equation and solve for x:
0 = (-2/3)x + 4
(2/3)x = 4
x = 4 * (3/2) = 6
Therefore, the x-intercept is (6, 0).
Example 2: Determining if a point lies on the line
Let's check if the point (9, -2) lies on the line y = (-2/3)x + 4. We substitute the coordinates into the equation:
-2 = (-2/3)(9) + 4
-2 = -6 + 4
-2 = -2
Since the equation holds true, the point (9, -2) lies on the line.
Example 3: Finding the equation of a parallel line
A line parallel to y = (-2/3)x + 4 will have the same slope, -2/3. If this parallel line passes through the point (3, 5), we can use the point-slope form to find its equation:
y - 5 = (-2/3)(x - 3)
y - 5 = (-2/3)x + 2
y = (-2/3)x + 7
Example 4: Finding the equation of a perpendicular line
A line perpendicular to y = (-2/3)x + 4 will have a slope that is the negative reciprocal of -2/3, which is 3/2. If this perpendicular line passes through the point (0, 0), its equation is:
y - 0 = (3/2)(x - 0)
y = (3/2)x
These examples illustrate the power and versatility of the slope-intercept form in solving various linear equation problems.
Conclusion
Converting the equation 2x + 3y = 12 to its slope-intercept form, y = (-2/3)x + 4, unlocks a wealth of information about the line it represents. Understanding the slope and y-intercept simplifies graphing, facilitates problem-solving, and opens doors to advanced applications in various fields. Mastering this conversion and the interpretation of the slope-intercept form is crucial for anyone working with linear equations and their applications. By practicing these techniques and exploring further examples, you can build a strong foundation in linear algebra and its practical implications.
Latest Posts
Latest Posts
-
What Percent Of 8 Is 7
Apr 03, 2025
-
One Degree Celsius Is Equal To How Many Degrees Fahrenheit
Apr 03, 2025
-
What Is The Diploid Number Of Chromosomes In Corn
Apr 03, 2025
-
What Is It Called When Liquid Changes To Gas
Apr 03, 2025
-
What Is 1 Percent Of 400
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about 2x 3y 12 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
