1 2 Divided By 1 6
listenit
May 25, 2025 · 5 min read
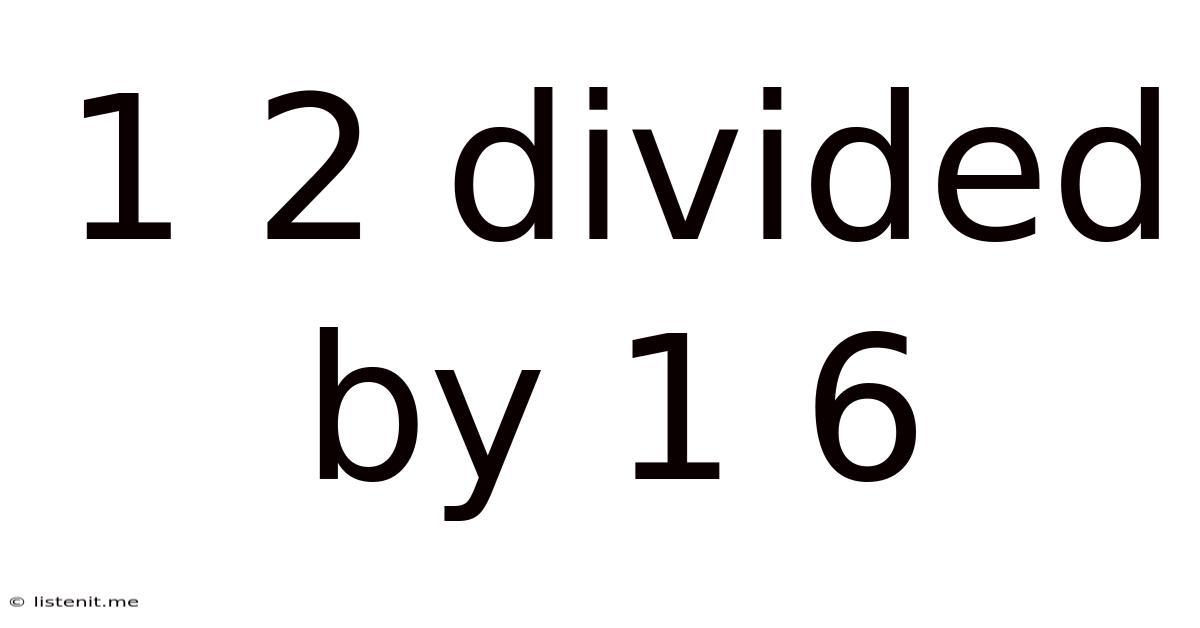
Table of Contents
1/2 Divided by 1/6: A Deep Dive into Fraction Division
This article explores the seemingly simple mathematical problem of dividing one fraction by another: 1/2 divided by 1/6. While the solution might seem straightforward, understanding the underlying principles is crucial for grasping more complex mathematical concepts. We will not only solve the problem but also delve into the 'why' behind the process, examining the concepts of reciprocals, fractions, and division itself. This comprehensive guide is designed for students, educators, and anyone looking to refresh their understanding of fractional arithmetic.
Understanding Fractions: The Building Blocks
Before tackling the division problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) represents two equal parts making up the whole. Understanding this fundamental concept is essential for navigating fraction division.
Reciprocals: The Key to Fraction Division
The concept of a reciprocal is central to dividing fractions. The reciprocal of a number is simply 1 divided by that number. For fractions, finding the reciprocal involves switching the numerator and the denominator.
For instance:
- The reciprocal of 1/2 is 2/1 (or simply 2).
- The reciprocal of 3/4 is 4/3.
- The reciprocal of 5 is 1/5.
Understanding reciprocals is the cornerstone of efficiently dividing fractions.
The "Keep, Change, Flip" Method: A Simple Approach
The most common method for dividing fractions is the "Keep, Change, Flip" (or "Keep, Switch, Flip") method. This method simplifies the process, making it easier to solve complex fraction division problems. Here's how it works:
- Keep: Keep the first fraction exactly as it is.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip (or find the reciprocal of) the second fraction.
Let's apply this method to our problem: 1/2 ÷ 1/6
- Keep: 1/2
- Change: ÷ becomes ×
- Flip: 1/6 becomes 6/1 (or simply 6)
This transforms the problem from 1/2 ÷ 1/6 to 1/2 × 6/1.
Multiplying Fractions: The Next Step
Now that we've converted the division problem into a multiplication problem, solving becomes significantly easier. Multiplying fractions involves multiplying the numerators together and the denominators together:
(1/2) × (6/1) = (1 × 6) / (2 × 1) = 6/2
Finally, simplify the resulting fraction:
6/2 = 3
Therefore, 1/2 divided by 1/6 equals 3.
Visualizing Fraction Division: A Concrete Example
Let's visualize this division using a real-world example. Imagine you have half a pizza (1/2). You want to divide this half-pizza into pieces that are each one-sixth (1/6) of a whole pizza. How many one-sixth pizza slices can you get from your half-pizza?
If a whole pizza is divided into 6 slices, then half a pizza contains 3 of these slices (3/6, which simplifies to 1/2). Therefore, you can get 3 slices of 1/6 from 1/2 a pizza. This visual representation confirms our mathematical solution.
Alternative Methods: Beyond "Keep, Change, Flip"
While the "Keep, Change, Flip" method is widely popular due to its simplicity, understanding the underlying mathematical principles offers alternative approaches. One such approach involves finding a common denominator:
-
Find a common denominator: For 1/2 and 1/6, the least common denominator is 6.
-
Convert fractions to equivalent fractions: 1/2 becomes 3/6 (by multiplying both numerator and denominator by 3).
-
Rewrite the problem: The problem becomes 3/6 ÷ 1/6.
-
Divide the numerators: Divide the numerators: 3 ÷ 1 = 3. This gives us the answer, 3.
Why Does "Keep, Change, Flip" Work? A Mathematical Explanation
The "Keep, Change, Flip" method isn't just a trick; it's a shortcut based on solid mathematical principles. Dividing by a fraction is equivalent to multiplying by its reciprocal. This stems from the definition of division: a ÷ b is the same as a × (1/b). The "Keep, Change, Flip" method effectively performs this multiplication by the reciprocal in a streamlined manner.
This method provides an efficient way to manipulate fractions during division without having to resort to more complex processes.
Real-World Applications: Where Fraction Division is Used
Fraction division isn't just a classroom exercise; it has numerous real-world applications:
- Cooking and Baking: Adjusting recipes to serve different numbers of people often involves fraction division.
- Construction and Engineering: Precise measurements in construction and engineering frequently require dividing fractions to ensure accuracy.
- Sewing and Quilting: Cutting fabric into specific pieces requires accurate calculations, often involving fraction division.
- Data Analysis: In statistical analysis, handling fractions and performing division are commonplace.
Troubleshooting Common Mistakes in Fraction Division
Several common mistakes can occur when dividing fractions:
- Forgetting to find the reciprocal: Students sometimes forget to flip the second fraction, leading to incorrect answers.
- Incorrectly multiplying fractions: Errors in multiplying the numerators and denominators can easily occur.
- Failing to simplify: Not simplifying the final fraction results in an unreduced and potentially confusing answer.
Practice Problems: Sharpening Your Skills
To solidify your understanding, let's try some practice problems:
- 2/3 ÷ 1/4 = ?
- 3/5 ÷ 2/5 = ?
- 1/8 ÷ 1/2 = ?
- 5/6 ÷ 5/12 = ?
- 1 1/2 ÷ 1/3 = ? (Remember to convert mixed numbers to improper fractions before solving)
Solving these problems will reinforce your understanding of the process and help you identify any areas where you might need further practice.
Conclusion: Mastering Fraction Division
Understanding fraction division is fundamental to many mathematical applications. By mastering the "Keep, Change, Flip" method or the common denominator method, you'll be well-equipped to handle fraction division with confidence. Remember that consistent practice and a strong grasp of the underlying mathematical principles are crucial for achieving proficiency. This detailed guide provides a comprehensive foundation for tackling not just 1/2 ÷ 1/6, but a wide range of fraction division problems, empowering you to confidently navigate this essential mathematical skill.
Latest Posts
Latest Posts
-
30 7 As A Mixed Number
May 25, 2025
-
What Is 25 Percent Of 30 Dollars
May 25, 2025
-
What Is 21 Days From Todays Date
May 25, 2025
-
What Is 4 2 In Simplest Form
May 25, 2025
-
How Many Days Are 4 Months
May 25, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Divided By 1 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.