What Is 25 Percent Of 30 Dollars
listenit
May 25, 2025 · 5 min read
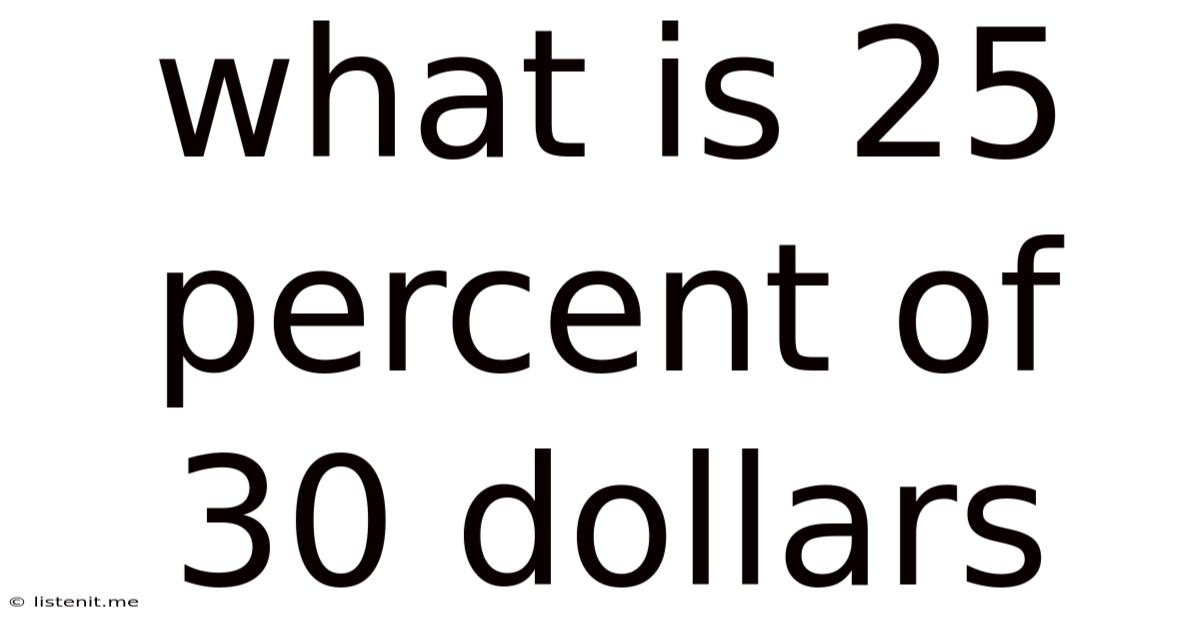
Table of Contents
What is 25 Percent of 30 Dollars? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with wide-ranging applications in everyday life, from budgeting and shopping to understanding financial reports and analyzing data. This article will delve into the seemingly simple question: "What is 25 percent of 30 dollars?" But we won't stop there. We'll explore the underlying mathematics, various calculation methods, real-world examples, and advanced applications of percentage calculations.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 25% is equivalent to 25/100, or 1/4, or 0.25 as a decimal. Understanding these equivalent forms is crucial for performing percentage calculations.
Calculating 25% of 30 Dollars: Three Methods
There are several ways to calculate 25% of 30 dollars. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is often the most straightforward method. We convert the percentage to its decimal equivalent (25% = 0.25) and multiply it by the total amount:
0.25 * $30 = $7.50
Therefore, 25% of 30 dollars is $\boxed{$7.50}$.
Method 2: Using Fractions
Since 25% is equivalent to 1/4, we can also solve this by dividing the total amount by 4:
$30 / 4 = $7.50
This method is particularly useful when dealing with percentages like 50%, 25%, 10%, or other simple fractions.
Method 3: Using Proportion
This method involves setting up a proportion:
25/100 = x/$30
To solve for x (25% of $30), we cross-multiply:
100x = 25 * $30 100x = $750 x = $750 / 100 x = $7.50
This method might seem more complex for this specific problem, but it's a powerful technique for solving more intricate percentage problems, especially when dealing with unknown variables.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-life scenarios:
-
Shopping and Sales: Discount percentages are ubiquitous in retail. Understanding how to calculate discounts helps you determine the final price after a sale. For example, a 20% discount on a $50 item can be calculated as 0.20 * $50 = $10 discount, resulting in a final price of $40.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Calculating the tax amount on a purchase or determining your tax liability requires accurate percentage calculations.
-
Tips and Gratuities: Calculating tips in restaurants or service charges often involves percentages. A 15% tip on a $60 meal is 0.15 * $60 = $9.
-
Financial Planning: Understanding interest rates (expressed as percentages), calculating returns on investments, and managing budgets all rely heavily on percentage calculations.
-
Data Analysis: Percentages are frequently used to represent proportions and trends in data. For example, analyzing market share, survey results, and population statistics often involves working with percentages.
-
Science and Engineering: Percentages play a crucial role in various scientific and engineering fields, such as expressing concentrations of solutions, measuring error margins, and calculating efficiency.
Advanced Percentage Calculations: Beyond the Basics
While calculating 25% of 30 dollars is straightforward, many real-world problems involve more complex scenarios. Here are some examples:
-
Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two values. For instance, if the price of an item increased from $20 to $25, the percentage increase is calculated as: (($25 - $20) / $20) * 100% = 25%.
-
Calculating the Original Amount: If you know the final amount after a percentage increase or decrease, you can work backward to find the original amount. For example, if a price increased by 10% to $33, the original price was $30 ($33 / 1.10 = $30).
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. Compound interest is a powerful concept in finance, and mastering its calculation is crucial for understanding investments and loans.
-
Percentage Points vs. Percentage Change: It's important to distinguish between these two concepts. A change of 5 percentage points is different from a 5% change. For example, increasing from 10% to 15% is a 5 percentage point increase but a 50% percentage increase (5/10 * 100%).
Mastering Percentage Calculations: Tips and Resources
Here are some tips to improve your skills in percentage calculations:
-
Practice Regularly: The best way to become proficient is to practice regularly with a variety of problems.
-
Use Multiple Methods: Familiarize yourself with different methods (decimal, fraction, proportion) to find the approach that best suits the problem.
-
Check Your Work: Always verify your answers to ensure accuracy.
-
Utilize Online Calculators (for verification only): Online percentage calculators can be useful for checking your work, but it's crucial to understand the underlying principles and be able to perform calculations manually.
-
Focus on Understanding Concepts: Don't just memorize formulas; strive to understand the concepts behind percentage calculations. This will allow you to adapt your skills to different situations and solve more complex problems.
Conclusion: The Power of Percentages
Understanding and mastering percentage calculations is a valuable skill with broad applications in various aspects of life. While the seemingly simple question of "What is 25% of 30 dollars?" serves as a starting point, the underlying principles extend far beyond this basic calculation. By mastering these principles, you can confidently tackle more complex percentage problems, improve your financial literacy, and enhance your analytical abilities in numerous fields. The ability to quickly and accurately calculate percentages is a cornerstone of numerical literacy and a valuable asset in the modern world.
Latest Posts
Latest Posts
-
1 3 5 7 11 13
May 25, 2025
-
What Is The Gcf Of 8 And 28
May 25, 2025
-
Btu To Heat 1000 Square Feet
May 25, 2025
-
What Is 30 Percent Of 200000
May 25, 2025
-
What Is Half Of 1 4 In Fraction Form
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Percent Of 30 Dollars . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.