1 3 5 7 11 13
listenit
May 25, 2025 · 6 min read
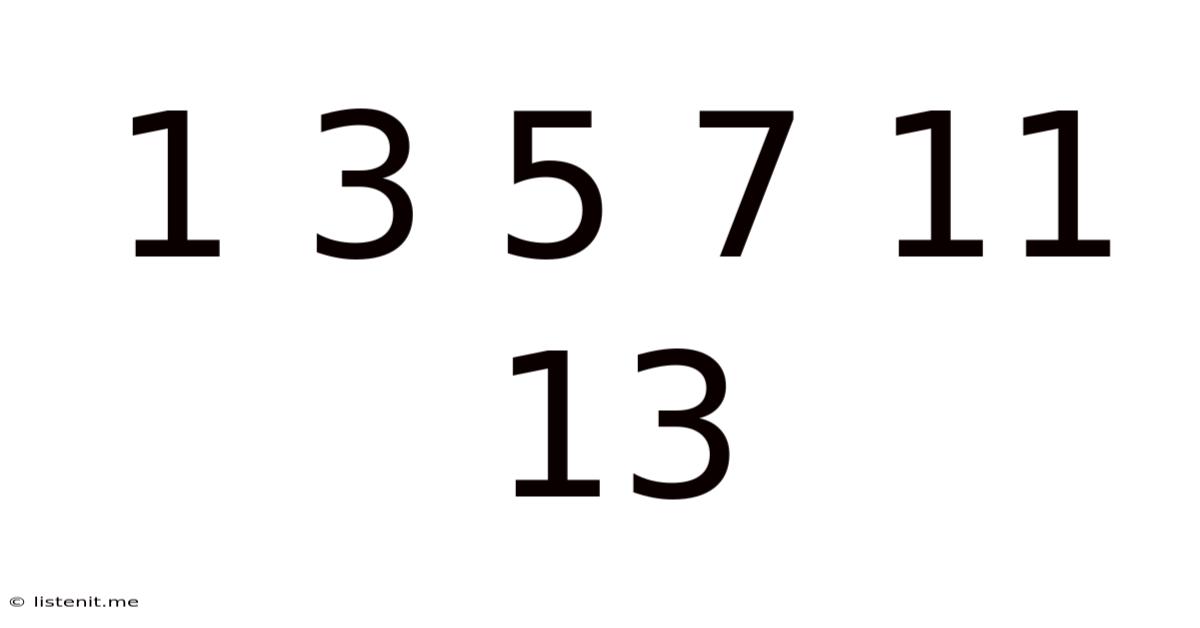
Table of Contents
Decoding the Sequence: 1 3 5 7 11 13 and the Allure of Prime Numbers
The seemingly simple sequence, 1, 3, 5, 7, 11, 13… holds a fascinating depth, captivating mathematicians and number enthusiasts for centuries. At first glance, it appears to be a straightforward list of odd numbers. However, a closer inspection reveals a deeper mathematical truth: it's a sequence of prime numbers (with the arguable exception of 1, which is neither prime nor composite). This article delves into the world of prime numbers, exploring their significance, properties, and the ongoing quest to understand their distribution within the sequence of natural numbers.
What are Prime Numbers?
Before diving into the specifics of our sequence, let's define the core concept: prime numbers. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In other words, it's only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and so on. They form the building blocks of all other integers through a process called prime factorization. Any composite number (a number that is not prime) can be uniquely expressed as a product of prime numbers. For example, 12 = 2 x 2 x 3, and 35 = 5 x 7.
The Exception of 1: A Prime Number or Not?
The inclusion of 1 in our initial sequence warrants some discussion. Mathematicians generally exclude 1 from the list of prime numbers. While it's divisible only by 1 and itself, including 1 would break the fundamental theorem of arithmetic – the unique prime factorization theorem. If 1 were considered prime, then numbers would have infinitely many prime factorizations, undermining the theorem's elegance and utility. Therefore, while 1 might seem like a natural addition to the sequence of odd numbers, it's excluded from the realm of primes to maintain mathematical consistency.
The Importance of Prime Numbers in Mathematics
Prime numbers are fundamental to number theory and have far-reaching applications in other areas of mathematics and beyond. Their seemingly random distribution presents a significant challenge and a source of ongoing research. Their importance stems from several key characteristics:
- Fundamental Theorem of Arithmetic: As mentioned earlier, every integer greater than 1 can be expressed uniquely as a product of prime numbers. This is the cornerstone of many number-theoretic arguments and computations.
- Cryptography: Prime numbers play a crucial role in modern cryptography, particularly in public-key cryptography systems like RSA. The difficulty of factoring large numbers into their prime components forms the basis of the security of these systems.
- Coding Theory: Prime numbers are used in designing error-correcting codes, which are essential for reliable data transmission and storage.
- Hashing Algorithms: Prime numbers are often employed in hashing algorithms, which are used to efficiently organize and search data in computer science.
The Distribution of Prime Numbers: An Ongoing Mystery
One of the most intriguing aspects of prime numbers is their seemingly unpredictable distribution among the natural numbers. While there are infinitely many prime numbers (a fact proven by Euclid), there's no simple formula to predict the exact location of the next prime. This unpredictability has fueled centuries of mathematical investigation, leading to significant advancements in number theory.
The Prime Number Theorem
The Prime Number Theorem provides an approximation of the distribution of primes. It states that the number of primes less than or equal to a given number x is approximately x / ln(x), where ln(x) is the natural logarithm of x. This theorem offers a valuable insight into the asymptotic density of prime numbers, even though it doesn't pinpoint the exact location of individual primes.
Gaps Between Prime Numbers: Twin Primes and More
The differences between consecutive prime numbers are called prime gaps. The study of prime gaps reveals fascinating patterns and open questions. Twin primes, which are pairs of prime numbers that differ by 2 (e.g., 3 and 5, 11 and 13), are a particularly intriguing area of research. The twin prime conjecture, which proposes that there are infinitely many twin primes, remains one of the most challenging unsolved problems in mathematics. Similarly, the study of larger prime gaps, and the distribution of gaps of different sizes, continue to fascinate mathematicians.
The Sequence 1, 3, 5, 7, 11, 13: A Glimpse into the World of Primes
Returning to our initial sequence, 1, 3, 5, 7, 11, 13, we can see it as a small window into the vast and complex world of prime numbers. While it only contains the first few primes (excluding 1), it illustrates the fundamental characteristics of these numbers:
- Odd Numbers (Except 2): With the exception of 2, all prime numbers are odd. This is because any even number greater than 2 is divisible by 2 and therefore not prime.
- Increasing Gaps: Notice that the gaps between consecutive primes in the sequence increase: 2, 2, 2, 4, 2. This illustrates that the distribution of primes is not uniform.
- The Search for Patterns: The quest for identifying predictable patterns in the distribution of prime numbers has driven mathematical research for centuries. While we may not have a complete understanding, the study of prime sequences like this one contributes to our knowledge.
Further Exploration: Advanced Concepts Related to Prime Numbers
The study of prime numbers extends far beyond the basics. Several advanced topics further deepen our understanding of these enigmatic numbers:
- Mersenne Primes: Mersenne primes are prime numbers that are one less than a power of 2 (e.g., 3, 7, 31). The search for Mersenne primes has been aided by powerful computing resources and remains an active area of research. The Great Internet Mersenne Prime Search (GIMPS) is a distributed computing project that has discovered many of the largest known primes.
- Fermat Primes: Fermat primes are prime numbers of the form 2<sup>2<sup>n</sup></sup> + 1, where n is a non-negative integer. Only five Fermat primes are currently known.
- Riemann Hypothesis: The Riemann Hypothesis is one of the most important unsolved problems in mathematics. It deals with the distribution of prime numbers and has profound implications for many areas of mathematics.
Conclusion: The Enduring Allure of Prime Numbers
The sequence 1, 3, 5, 7, 11, 13, while seemingly simple at first glance, provides a gateway to the rich and fascinating world of prime numbers. From their fundamental role in number theory to their critical applications in cryptography and computer science, prime numbers continue to intrigue mathematicians and researchers. The unpredictable nature of their distribution, coupled with their profound mathematical significance, ensures that the exploration of prime numbers will remain a vibrant and active field of inquiry for generations to come. The quest to unravel the secrets hidden within these fundamental building blocks of numbers remains one of mathematics’ most captivating challenges, driving innovation and inspiring new discoveries along the way. The simple sequence 1, 3, 5, 7, 11, 13 serves as a powerful reminder of the enduring allure of these enigmatic numbers and the boundless mysteries they still hold.
Latest Posts
Latest Posts
-
How Many Days Since May 26th
May 25, 2025
-
What Is 3 4 Divided By 6
May 25, 2025
-
40 Out Of 60 In Percentage
May 25, 2025
-
What Is Half Of 3 4 In Fraction Form
May 25, 2025
-
What Year Was I Born If Im 57
May 25, 2025
Related Post
Thank you for visiting our website which covers about 1 3 5 7 11 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.