40 Out Of 60 In Percentage
listenit
May 25, 2025 · 5 min read
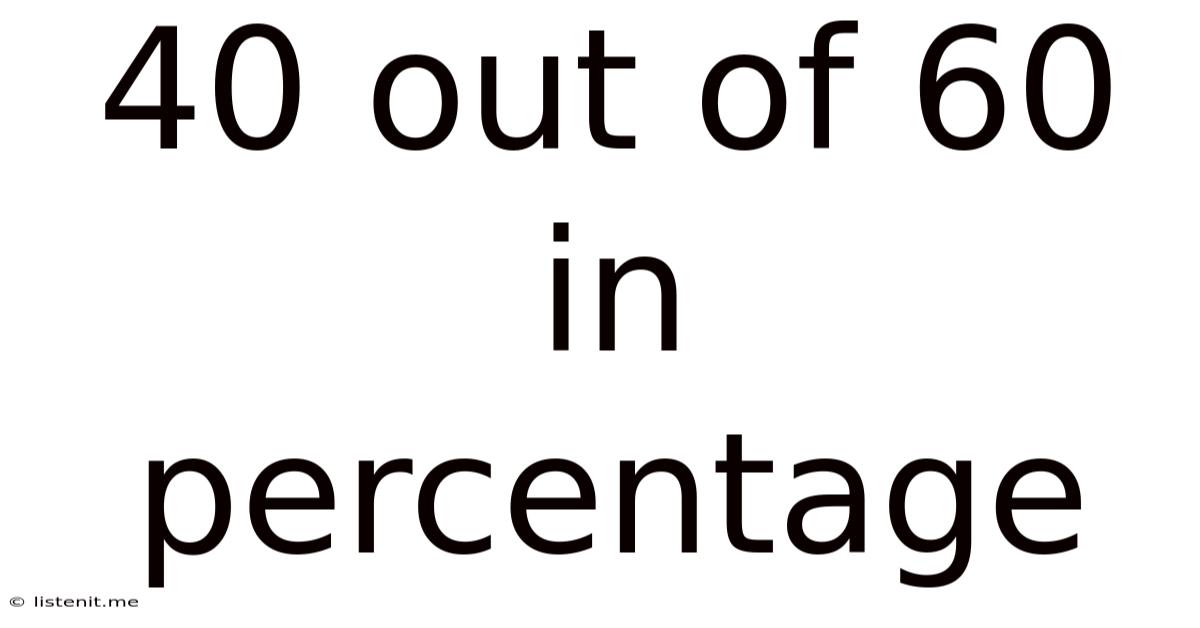
Table of Contents
40 out of 60 in Percentage: A Comprehensive Guide to Understanding and Calculating Percentages
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial transactions and everyday life scenarios. Understanding how to calculate percentages accurately and efficiently is crucial for informed decision-making and problem-solving. This comprehensive guide dives deep into the calculation of 40 out of 60 as a percentage, providing multiple methods, practical applications, and related concepts to solidify your understanding.
Understanding the Basics of Percentage Calculations
Before we delve into the specific calculation of 40 out of 60, let's review the fundamental principles of percentage calculations. A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred." The symbol used to represent percentage is %.
The basic formula for calculating a percentage is:
(Part / Whole) x 100 = Percentage
Where:
- Part: Represents the specific value you're interested in expressing as a percentage of the whole.
- Whole: Represents the total value or the complete amount.
Calculating 40 out of 60 as a Percentage: Method 1 - The Basic Formula
Applying the basic formula to calculate 40 out of 60 as a percentage:
(40 / 60) x 100 = Percentage
-
Divide the part by the whole: 40 divided by 60 equals 0.6667 (approximately).
-
Multiply by 100: 0.6667 multiplied by 100 equals 66.67%.
Therefore, 40 out of 60 is 66.67%.
Calculating 40 out of 60 as a Percentage: Method 2 - Simplification
This method involves simplifying the fraction before converting it to a percentage. This can make the calculation easier, especially with larger numbers.
-
Simplify the fraction: The fraction 40/60 can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 20. This simplifies the fraction to 2/3.
-
Convert the simplified fraction to a decimal: 2 divided by 3 equals 0.6667 (approximately).
-
Multiply by 100: 0.6667 multiplied by 100 equals 66.67%.
Again, we arrive at the same result: 40 out of 60 is 66.67%.
Calculating 40 out of 60 as a Percentage: Method 3 - Using a Calculator
Most calculators have a percentage function that simplifies the process. Simply enter 40, then the division symbol, then 60, and finally the percentage symbol (%). The calculator will directly display the result: 66.67%.
Practical Applications of Percentage Calculations: Real-World Examples
Understanding percentage calculations is crucial in various real-life scenarios. Here are a few examples:
1. Academic Performance
Imagine a student scored 40 out of 60 marks in an exam. Using the methods described above, we know this translates to 66.67%. This percentage allows for easy comparison with other students' scores and helps assess overall performance.
2. Sales and Discounts
Stores often advertise discounts as percentages. For instance, a 40% discount on an item initially priced at $60 means a reduction of (40/100) x $60 = $24. The final price after the discount would be $60 - $24 = $36.
3. Financial Calculations
Percentage calculations are fundamental in finance. Interest rates on loans, investments, and savings accounts are typically expressed as percentages. Calculating interest earned or paid requires understanding percentage calculations.
4. Surveys and Statistics
Surveys and polls often present results as percentages. For example, if 40 out of 60 respondents answered "yes" to a particular question, the percentage of "yes" responses would be 66.67%. This enables easy interpretation and comparison of survey data.
5. Everyday Life
Percentage calculations are useful in various everyday situations, such as calculating tips in restaurants, determining the percentage of ingredients in a recipe, or understanding tax rates.
Beyond the Basics: Understanding Percentage Increase and Decrease
Understanding how to calculate percentage increase and decrease is an essential extension of basic percentage calculations.
Percentage Increase: To calculate the percentage increase, use the following formula:
[(New Value - Original Value) / Original Value] x 100 = Percentage Increase
Percentage Decrease: To calculate the percentage decrease, use this formula:
[(Original Value - New Value) / Original Value] x 100 = Percentage Decrease
Let's illustrate with an example:
If the price of an item increases from $40 to $60, the percentage increase is:
[($60 - $40) / $40] x 100 = 50%
Conversely, if the price decreases from $60 to $40, the percentage decrease is:
[($60 - $40) / $60] x 100 = 33.33%
Advanced Percentage Calculations: Working with Multiple Percentages
Sometimes, you need to work with multiple percentages in a single calculation. For example, you might need to calculate a series of discounts or interest rates compounded over time. These calculations require a careful step-by-step approach.
Let's say an item is initially priced at $100. It receives a 20% discount, followed by an additional 10% discount. To calculate the final price:
- First discount: $100 x (1 - 0.20) = $80
- Second discount: $80 x (1 - 0.10) = $72
The final price after both discounts is $72. Note that this is not the same as applying a 30% discount directly ($100 x (1 - 0.30) = $70). The order of discounts and the nature of the discounts (e.g., successive discounts vs discounts on already-discounted price) matter.
Error Analysis and Common Mistakes in Percentage Calculations
Common mistakes in percentage calculations include:
- Incorrect order of operations: Remember to perform the division before multiplication when using the basic percentage formula.
- Rounding errors: Rounding numbers prematurely can lead to inaccuracies in the final result. It's best to use the full decimal value during calculations and round only the final answer.
- Confusing percentage increase and decrease: Understand the difference between the formulas for calculating percentage increase and percentage decrease.
- Incorrect application of multiple percentages: Be mindful of the order and method when calculating multiple percentages.
Conclusion: Mastering Percentage Calculations for Success
Mastering percentage calculations is a valuable skill that enhances your problem-solving abilities in various aspects of life. Whether you are tackling academic assignments, managing finances, or navigating everyday situations, understanding percentages empowers you to make informed decisions and interpret data accurately. Remember the fundamental formula, practice different methods, and always double-check your calculations to avoid common errors. By consistently applying these principles, you can build confidence and competence in tackling all sorts of percentage problems. The detailed explanation and practical examples provided in this guide will serve as a valuable resource for your ongoing learning journey in mastering percentage calculations.
Latest Posts
Latest Posts
-
1 2 Plus 1 2 Equals
May 25, 2025
-
How Many Days In 3 Year
May 25, 2025
-
30 Days After November 22 2024
May 25, 2025
-
What Is 8 15 As A Grade
May 25, 2025
-
What Percent Is 14 Of 24
May 25, 2025
Related Post
Thank you for visiting our website which covers about 40 Out Of 60 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.