30 7 As A Mixed Number
listenit
May 25, 2025 · 4 min read
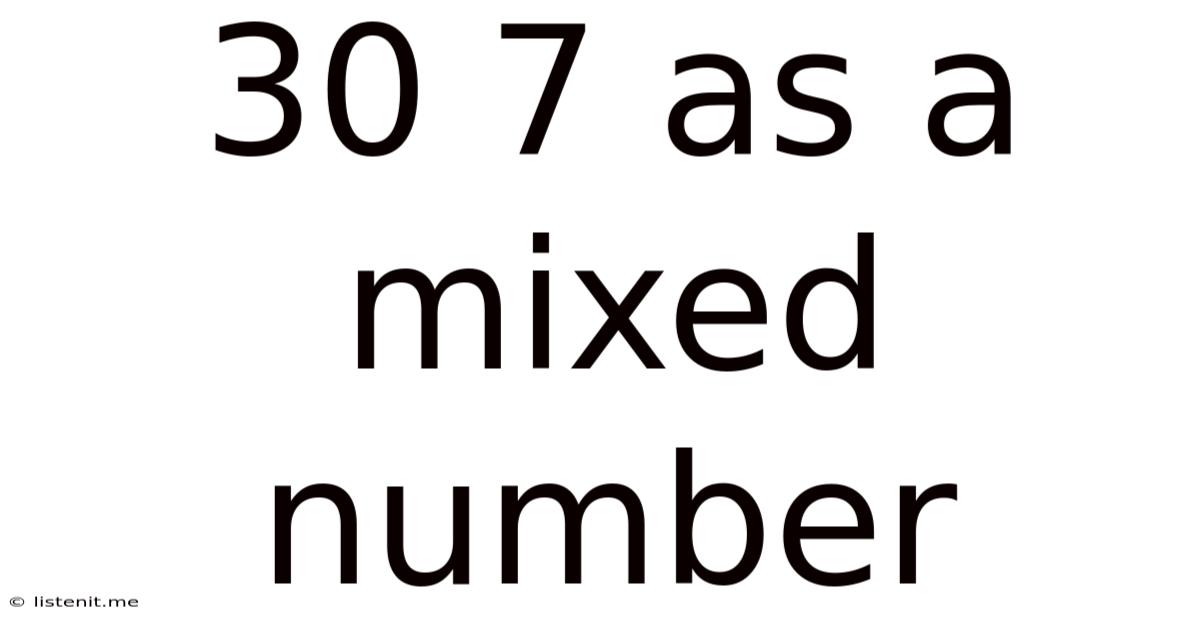
Table of Contents
30/7 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 30/7 into a mixed number, explaining the concepts involved and offering various approaches to solve similar problems. We'll also explore the importance of understanding mixed numbers in real-world applications and discuss related mathematical concepts.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number, where 2 is the whole number and ¾ is the proper fraction.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. The fraction 30/7 is an example of an improper fraction because the numerator (30) is larger than the denominator (7). Improper fractions represent values greater than or equal to one.
Converting 30/7 to a Mixed Number: The Division Method
The most straightforward method for converting an improper fraction to a mixed number is through division. We divide the numerator (30) by the denominator (7).
-
Perform the division: 30 ÷ 7 = 4 with a remainder of 2.
-
Identify the whole number: The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the whole number is 4.
-
Identify the fraction: The remainder (the number left over after the division) becomes the numerator of the proper fraction. The denominator remains the same as the original fraction. Therefore, the fraction is 2/7.
-
Combine the whole number and fraction: Combine the whole number and the proper fraction to create the mixed number. Thus, 30/7 as a mixed number is 4 2/7.
Visualizing the Conversion
Imagine you have 30 cookies, and you want to divide them equally among 7 friends. You can give each friend 4 cookies (4 x 7 = 28 cookies). You'll have 2 cookies left over (30 - 28 = 2). This represents 4 whole sets of cookies (the whole number) and 2/7 of a set (the fraction).
Alternative Methods: Repeated Subtraction
While division is the most efficient method, you can also use repeated subtraction to convert 30/7 to a mixed number.
-
Subtract the denominator from the numerator repeatedly: Start by subtracting 7 from 30. 30 - 7 = 23. Repeat this process: 23 - 7 = 16; 16 - 7 = 9; 9 - 7 = 2.
-
Count the subtractions: You subtracted 7 four times before reaching a remainder less than 7. This 4 represents the whole number.
-
The remainder is the numerator: The remaining 2 becomes the numerator of the fraction.
-
The denominator remains unchanged: The denominator remains 7.
Therefore, the mixed number is again 4 2/7.
Why is Understanding Mixed Numbers Important?
Mixed numbers are crucial in various real-world scenarios and mathematical applications:
-
Measurement: Measuring lengths, weights, or volumes often results in mixed numbers (e.g., 2 ½ inches, 3 ¼ pounds).
-
Cooking and Baking: Recipes frequently use mixed numbers to specify ingredient quantities (e.g., 1 ½ cups of flour).
-
Time: Time is often expressed using mixed numbers (e.g., 2 ½ hours).
-
Geometry and Algebra: Mixed numbers appear in various geometrical calculations and algebraic expressions.
-
Data Analysis: When working with averages or other statistical data, mixed numbers might arise in the results.
-
Everyday Life: Numerous daily tasks involve fractions and mixed numbers, making their comprehension essential for practical problem-solving.
Further Exploration: Working with Mixed Numbers
Once you've converted an improper fraction to a mixed number, you can perform various operations, such as:
-
Addition and Subtraction of Mixed Numbers: Requires finding a common denominator for the fractional parts before adding or subtracting the whole numbers and fractions separately.
-
Multiplication and Division of Mixed Numbers: Often simplifies by converting the mixed numbers back into improper fractions before performing the operation.
-
Comparing Mixed Numbers: Compares whole number parts first, then fractional parts if the whole numbers are equal.
Examples of Converting Improper Fractions to Mixed Numbers:
Let's practice with a few more examples:
-
15/4: 15 ÷ 4 = 3 with a remainder of 3. Therefore, 15/4 = 3 ¾
-
22/5: 22 ÷ 5 = 4 with a remainder of 2. Therefore, 22/5 = 4 2/5
-
37/8: 37 ÷ 8 = 4 with a remainder of 5. Therefore, 37/8 = 4 5/8
-
41/6: 41 ÷ 6 = 6 with a remainder of 5. Therefore, 41/6 = 6 5/6
Conclusion:
Converting improper fractions to mixed numbers is a fundamental mathematical skill with practical applications in numerous fields. By mastering this conversion, along with understanding the concepts of proper and improper fractions, you'll be well-equipped to handle a wide range of mathematical problems and real-world situations effectively. Remember, the division method provides the most efficient approach, but repeated subtraction offers an alternative understanding of the process. Practice makes perfect – so work through several examples to solidify your understanding and build confidence in your mathematical abilities. The ability to comfortably navigate fractions and mixed numbers is a key component of mathematical literacy and a valuable asset in everyday life.
Latest Posts
Latest Posts
-
32 A Bra Size In Cm
May 25, 2025
-
Write 94 As A Fraction In Simplest Form
May 25, 2025
-
7 4 9 As An Improper Fraction
May 25, 2025
-
What Is The Prime Factorization Of 59
May 25, 2025
-
What Is 4 8 In A Fraction
May 25, 2025
Related Post
Thank you for visiting our website which covers about 30 7 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.