X 2 Y 2 Z 2 1
listenit
Jun 14, 2025 · 5 min read
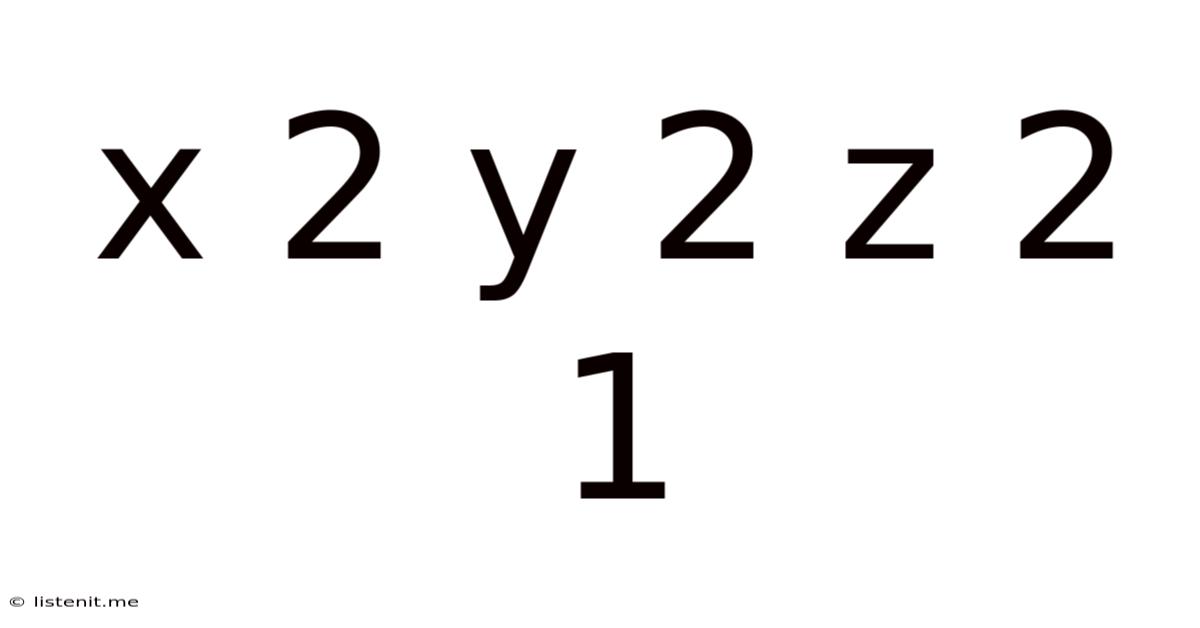
Table of Contents
Exploring the Equation x² + y² + z² = 1: A Deep Dive into its Mathematical and Geometric Implications
The seemingly simple equation, x² + y² + z² = 1, holds a wealth of mathematical richness and geometrical significance. At first glance, it might appear straightforward, but a closer examination reveals its deep connections to various mathematical fields, offering a fascinating exploration for mathematicians and enthusiasts alike. This article delves into the intricacies of this equation, unpacking its properties, interpretations, and applications.
Understanding the Fundamental Nature of the Equation
The equation x² + y² + z² = 1 represents a unit sphere in three-dimensional Euclidean space. This means that any point (x, y, z) that satisfies the equation lies exactly one unit away from the origin (0, 0, 0). The sphere's center is located at the origin, and its radius is 1.
Geometric Interpretation: The Unit Sphere
The most immediate interpretation is its geometric representation as a sphere. Imagine a three-dimensional coordinate system. The equation defines the surface of a sphere with a radius of one unit centered at the origin. Every point (x, y, z) on this surface satisfies the equation, and any point outside or inside the sphere does not. This visual representation allows for an intuitive understanding of the equation's properties.
Mathematical Implications: Pythagorean Theorem in 3D
The equation is a three-dimensional extension of the Pythagorean theorem. In two dimensions, the Pythagorean theorem states that the square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides. Our equation extends this concept to three dimensions: the sum of the squares of the three orthogonal distances (x, y, z) from the origin is equal to the square of the distance from the origin to the point (x, y, z) on the sphere’s surface (which is 1).
Delving Deeper: Exploring Advanced Concepts
Beyond its basic geometrical interpretation, the equation x² + y² + z² = 1 opens doors to more complex mathematical concepts and applications.
Spherical Coordinates: A Different Perspective
The equation can be elegantly represented using spherical coordinates, a coordinate system that simplifies calculations involving spheres. In spherical coordinates, a point (x, y, z) is represented by (ρ, θ, φ), where ρ is the radial distance from the origin, θ is the azimuthal angle (longitude), and φ is the polar angle (colatitude). For our unit sphere, ρ = 1, leading to a simplified representation that emphasizes the angular aspects of points on the sphere's surface.
Surface Area and Volume Calculations
The equation allows us to calculate the surface area and volume of the unit sphere. Using integral calculus, the surface area is found to be 4π, and the volume is (4/3)π. These are fundamental results in geometry and have numerous applications in various scientific and engineering fields.
Parameterization and Vector Functions
The equation can be parameterized using various techniques, enabling the representation of the sphere’s surface using vector functions. This is crucial in areas like computer graphics, where representing and manipulating three-dimensional objects is essential. Parameterizations allow for the generation of points on the sphere's surface for rendering and animation purposes. One common parameterization uses spherical coordinates:
x = sin(φ)cos(θ) y = sin(φ)sin(θ) z = cos(φ)
where 0 ≤ φ ≤ π and 0 ≤ θ ≤ 2π.
Applications in Physics and Engineering
The unit sphere equation is central to various areas of physics and engineering.
- Electromagnetism: The equation plays a significant role in understanding electric and magnetic fields, especially in scenarios involving spherical symmetry.
- Quantum Mechanics: In quantum mechanics, the unit sphere appears in the context of representing the state space of a quantum system, often visualized as a Bloch sphere.
- Signal Processing: The sphere is utilized in representing signals in higher dimensions.
- Computer Graphics: As mentioned earlier, parameterizations of this equation are critical in generating 3D models and animations of spherical objects.
- Astronomy and Celestial Mechanics: Spherical coordinates, directly derived from the unit sphere, are invaluable for modeling celestial bodies and their movements.
Extending the Equation: Generalizations and Variations
The fundamental equation can be generalized and modified to explore related concepts.
Hyper-spheres in Higher Dimensions
The equation can be extended to higher dimensions. In n-dimensional space, the equation x₁² + x₂² + ... + xₙ² = 1 represents an (n-1)-dimensional hypersphere. These hyperspheres are complex mathematical objects with properties that extend and generalize the concepts we've discussed for the 3D sphere.
Ellipsoids: A Modification of the Equation
By introducing scaling factors to the x, y, and z terms, we can transform the unit sphere into an ellipsoid. This changes the shape while maintaining the fundamental concept of a curved surface defined by a quadratic equation. The general equation for an ellipsoid is:
(x²/a²) + (y²/b²) + (z²/c²) = 1
where 'a', 'b', and 'c' are the semi-major axes along the x, y, and z directions respectively.
Applications in Statistics and Data Analysis
Variations of the equation appear in statistical analysis, particularly in multivariate data analysis. For example, the Mahalanobis distance, a measure of the distance between a point and a distribution, involves a quadratic form similar to our equation, allowing for the analysis of data points in multi-dimensional spaces.
Conclusion: A Simple Equation with Profound Implications
The seemingly simple equation x² + y² + z² = 1, representing the unit sphere, serves as a gateway to a vast array of mathematical concepts and practical applications. From its fundamental geometric interpretation as a sphere to its advanced applications in physics, engineering, and data analysis, this equation showcases the power and beauty of mathematics in its ability to model and describe the world around us. The exploration of this equation is not merely an exercise in abstract mathematics; it’s a journey into the core principles that underpin our understanding of space, geometry, and numerous scientific phenomena. Its elegance and versatility continue to fascinate mathematicians and inspire new discoveries across diverse fields. Further research into its generalizations and variations promises even deeper insights into the mathematical structures and relationships that govern our universe.
Latest Posts
Latest Posts
-
Andre The Giant Holding A Beer
Jun 15, 2025
-
4 Wire Ceiling Fan Wiring Diagram
Jun 15, 2025
-
Mac Connecting To Wifi But No Internet
Jun 15, 2025
-
Does Alarm Work In Airplane Mode
Jun 15, 2025
-
Does Windshield Washer Fluid Go Bad
Jun 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 Z 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.