X 2 Xy Y 2 1
listenit
May 10, 2025 · 4 min read
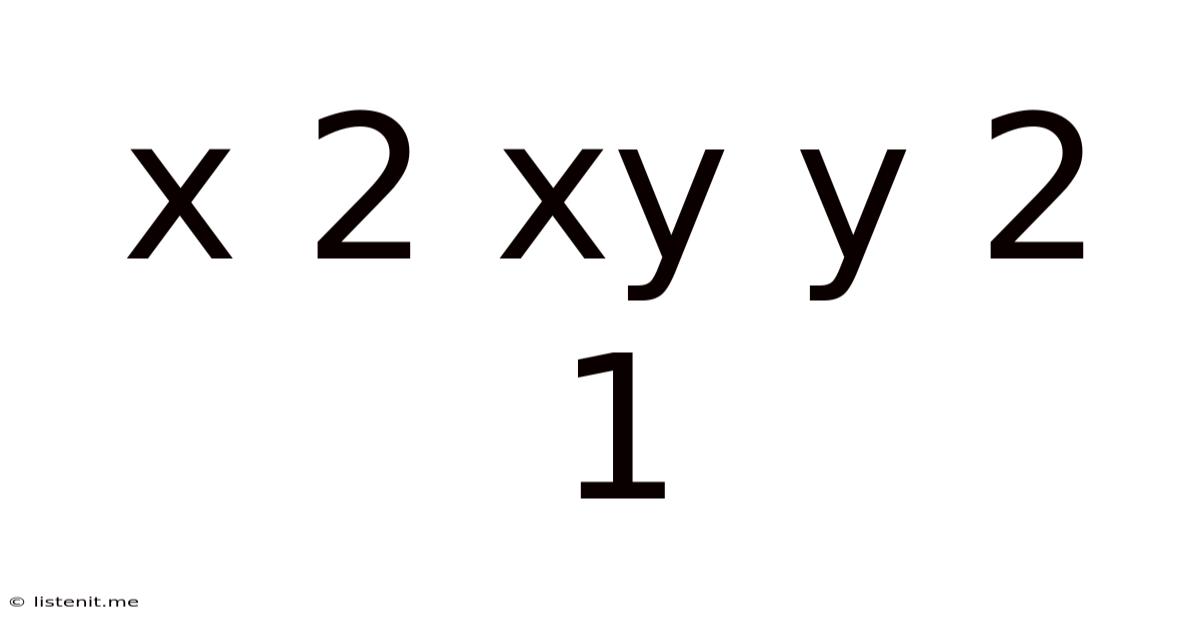
Table of Contents
Exploring the Equation x² + 2xy + y² = 1: A Deep Dive into Conics
The equation x² + 2xy + y² = 1 might seem deceptively simple at first glance. However, this seemingly unassuming quadratic equation hides a rich mathematical landscape, revealing fascinating geometrical properties and connections to various branches of mathematics. This article will explore this equation in detail, examining its graphical representation, algebraic manipulations, and the insights it offers into the world of conic sections.
Understanding the Equation: A Geometric Perspective
The equation x² + 2xy + y² = 1 represents a conic section. Conic sections are curves formed by the intersection of a plane and a double cone. Familiar examples include circles, ellipses, parabolas, and hyperbolas. The key to understanding the specific conic represented by our equation lies in recognizing its structure.
We can rewrite the equation as:
(x + y)² = 1
This factorization dramatically simplifies our understanding. The equation now clearly represents a pair of parallel lines. Specifically, it describes the lines:
- x + y = 1
- x + y = -1
These lines are parallel and separated by a distance of √2 units. This geometric interpretation is crucial for visualizing and analyzing the properties of the equation.
Graphical Representation and Key Features
Plotting the lines x + y = 1 and x + y = -1 on a Cartesian coordinate system reveals two straight lines with a slope of -1. The lines are equidistant from the origin, indicating a symmetrical arrangement. Key features of this graphical representation include:
- Parallelism: The most striking feature is the parallelism of the lines. This is a direct consequence of the equation's factored form.
- Symmetry: The lines exhibit symmetry with respect to the origin. Reflecting either line across the origin yields the other line.
- Intercept: Each line intersects the x and y axes at (1,0) and (0,1) and (-1,0) and (0,-1) respectively.
Algebraic Manipulations and Transformations
While the factored form (x + y)² = 1 provides the most straightforward geometric interpretation, exploring algebraic manipulations can yield further insights. Let's consider some transformations:
Rotation of Axes
We can rotate the coordinate system to simplify the equation. A rotation of axes by 45 degrees would eliminate the xy term. This transformation involves substituting:
- x = (x' - y')/√2
- y = (x' + y')/√2
Substituting these into the original equation and simplifying, we would obtain an equation of the form:
2x'² = 1 or x'² = 1/2
This represents two parallel lines parallel to the y'-axis, confirming our earlier geometric interpretation.
Translation of Axes
Translating the coordinate system doesn't alter the essential nature of the conic. Translation simply shifts the location of the lines without affecting their parallelism or slope.
Connections to Other Mathematical Concepts
The equation x² + 2xy + y² = 1 provides a valuable lens for exploring various mathematical concepts:
Linear Algebra
The equation can be represented using matrix notation. Consider the matrix:
A = [[1, 1],
[1, 1]]
Then the equation can be expressed as:
[x, y] A [x, y]ᵀ = 1
Analyzing the eigenvalues and eigenvectors of matrix A reveals further information about the conic section. The eigenvectors represent the directions of the principal axes, and the eigenvalues relate to the scaling along these axes.
Calculus
Calculus provides tools for analyzing the tangent lines to the lines represented by the equation. The slope of each line is -1, which remains consistent along the entire length of each line. This simplicity arises from the linearity of the equations.
Differential Equations
While not directly expressed as a differential equation, the equation can be related to systems of differential equations describing motion along the lines. The solutions to these equations would trace out the paths along the lines.
Applications and Real-World Examples
While the equation's graphical representation is relatively simple, its underlying concepts find applications in various fields:
Physics
Parallel lines are fundamental in classical mechanics, representing trajectories or constraints in certain systems. The equation's symmetry reflects scenarios with equal and opposite forces.
Engineering
In structural engineering, parallel lines can represent load-bearing members in a structure or directions of forces. The simplicity of the equation facilitates calculations of forces and stresses.
Advanced Considerations and Extensions
The exploration of x² + 2xy + y² = 1 can be extended to more complex scenarios:
Generalization to other Conics
By changing the constant term on the right-hand side (e.g., x² + 2xy + y² = k, where k is a constant), we can explore variations in the distance between the parallel lines. For k > 0, we maintain parallel lines. For k=0, the lines intersect at the origin, and for k<0, we have no real solutions.
Higher-Dimensional Analogues
The concept of parallel lines and the associated algebraic structure can be generalized to higher dimensions, leading to hyperplanes and more complex geometric objects.
Conclusion
The seemingly simple equation x² + 2xy + y² = 1 offers a rich and multifaceted exploration into the world of conic sections, linear algebra, and geometric transformations. Its simple graphical representation of parallel lines belies the deeper mathematical structures and potential applications that this equation encapsulates. Through algebraic manipulations, rotations, and translations, we can gain a comprehensive understanding of its properties and its connections to various mathematical fields. This exploration underscores the beauty and interconnectedness of mathematical concepts, highlighting the power of simple equations to reveal profound insights. Further research into generalizations and extensions of this equation can lead to even more fascinating discoveries.
Latest Posts
Latest Posts
-
How Many Energy Levels Does Sulfur Have
May 10, 2025
-
What Is The Lcm Of 10 And 14
May 10, 2025
-
Common Multiples Of 9 And 21
May 10, 2025
-
Can Polar Molecules Cross The Lipid Bilayer
May 10, 2025
-
Completely Factor The Expression 18x2 78x 60
May 10, 2025
Related Post
Thank you for visiting our website which covers about X 2 Xy Y 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.