What Is The Lcm Of 10 And 14
listenit
May 10, 2025 · 5 min read
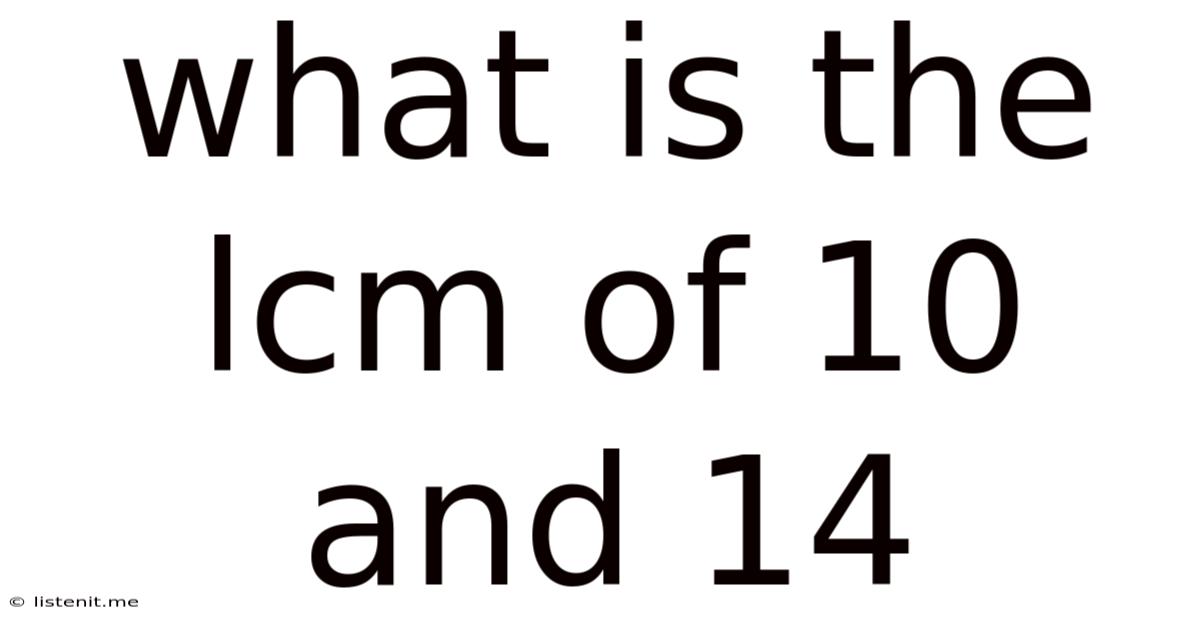
Table of Contents
What is the LCM of 10 and 14? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculation opens doors to more advanced mathematical concepts. This article delves into the intricacies of finding the LCM of 10 and 14, exploring different approaches, and highlighting their applications in various fields. We'll move beyond a simple answer to provide a comprehensive understanding of LCMs and their significance.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 10 and 14, let's solidify our understanding of what an LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12… and the multiples of 3 are 3, 6, 9, 12, 15… The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
This concept extends to more than two numbers. Finding the LCM is a crucial component in various mathematical operations and real-world applications.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of smaller numbers, like 10 and 14, is by listing their multiples.
Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140...
Multiples of 14: 14, 28, 42, 56, 70, 84, 98, 112, 126, 140...
By comparing the two lists, we can see that the smallest number common to both is 70. Therefore, the LCM of 10 and 14 is 70.
This method is simple for small numbers but becomes cumbersome and inefficient for larger numbers or a greater number of integers.
Method 2: Prime Factorization
A more efficient and systematic method for finding the LCM, especially for larger numbers, is through prime factorization. This method involves breaking down each number into its prime factors.
Prime Factorization of 10: 2 x 5
Prime Factorization of 14: 2 x 7
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations:
- 2: The highest power of 2 is 2¹ (present in both).
- 5: The highest power of 5 is 5¹ (present only in 10).
- 7: The highest power of 7 is 7¹ (present only in 14).
Now, multiply these highest powers together: 2 x 5 x 7 = 70
Therefore, the LCM of 10 and 14, using prime factorization, is 70. This method is considerably more efficient than listing multiples, especially when dealing with larger numbers.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers themselves. This relationship provides another method for calculating the LCM.
First, let's find the GCD of 10 and 14 using the Euclidean algorithm:
- Divide the larger number (14) by the smaller number (10): 14 ÷ 10 = 1 with a remainder of 4.
- Replace the larger number with the smaller number (10) and the smaller number with the remainder (4): 10 ÷ 4 = 2 with a remainder of 2.
- Repeat: 4 ÷ 2 = 2 with a remainder of 0.
The last non-zero remainder is the GCD, which is 2.
Now, using the relationship between LCM and GCD:
LCM(10, 14) = (10 x 14) / GCD(10, 14) = (140) / 2 = 70
This method is particularly useful when dealing with larger numbers where prime factorization might become more complex.
Applications of LCM in Real-World Scenarios
The seemingly abstract concept of LCM finds practical applications in various real-world scenarios:
-
Scheduling: Imagine two buses leave a terminal at different intervals. One bus leaves every 10 minutes, and another leaves every 14 minutes. The LCM (70 minutes) determines when both buses will depart simultaneously again.
-
Patterning: Consider repeating patterns in design or construction. If one pattern repeats every 10 units and another every 14 units, the LCM (70 units) determines when both patterns will align perfectly.
-
Fraction Operations: Finding the LCM is crucial when adding or subtracting fractions with different denominators. The LCM of the denominators becomes the common denominator, simplifying the calculation.
-
Gear Ratios: In mechanics, the LCM helps determine the least number of rotations required for gears with different numbers of teeth to return to their initial positions.
-
Music: Musical intervals and harmonies can be related to LCMs, influencing the creation of melodies and chords.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you simply consider all the prime factors of all the numbers involved and choose the highest power of each. For the GCD method, you can extend the Euclidean algorithm to work with more than two numbers. However, listing multiples becomes increasingly impractical as the number of integers increases.
Conclusion: Beyond the Simple Answer
While the answer to "What is the LCM of 10 and 14?" is simply 70, the journey to arrive at that answer has unveiled the richness and applicability of the LCM concept. Understanding different calculation methods, from listing multiples to prime factorization and utilizing the GCD, provides valuable mathematical insight. Moreover, appreciating the diverse real-world applications of LCM underscores its importance beyond the classroom, demonstrating its relevance in various fields and everyday scenarios. This in-depth exploration emphasizes the significance of not just obtaining the answer but grasping the underlying principles and their practical implications. The ability to efficiently and accurately calculate LCMs is a fundamental skill with far-reaching consequences in numerous areas of study and professional practice.
Latest Posts
Latest Posts
-
The Variables X And Y Vary Inversely
May 10, 2025
-
Interconverting The Wavelength And Frequency Of Electromagnetic Radiation
May 10, 2025
-
40 As A Decimal And Fraction
May 10, 2025
-
What Is The Major Difference Between Primary And Secondary Succession
May 10, 2025
-
The Lanthanides And Actinides Belong Between
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 10 And 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.