Completely Factor The Expression 18x2 - 78x - 60.
listenit
May 10, 2025 · 4 min read
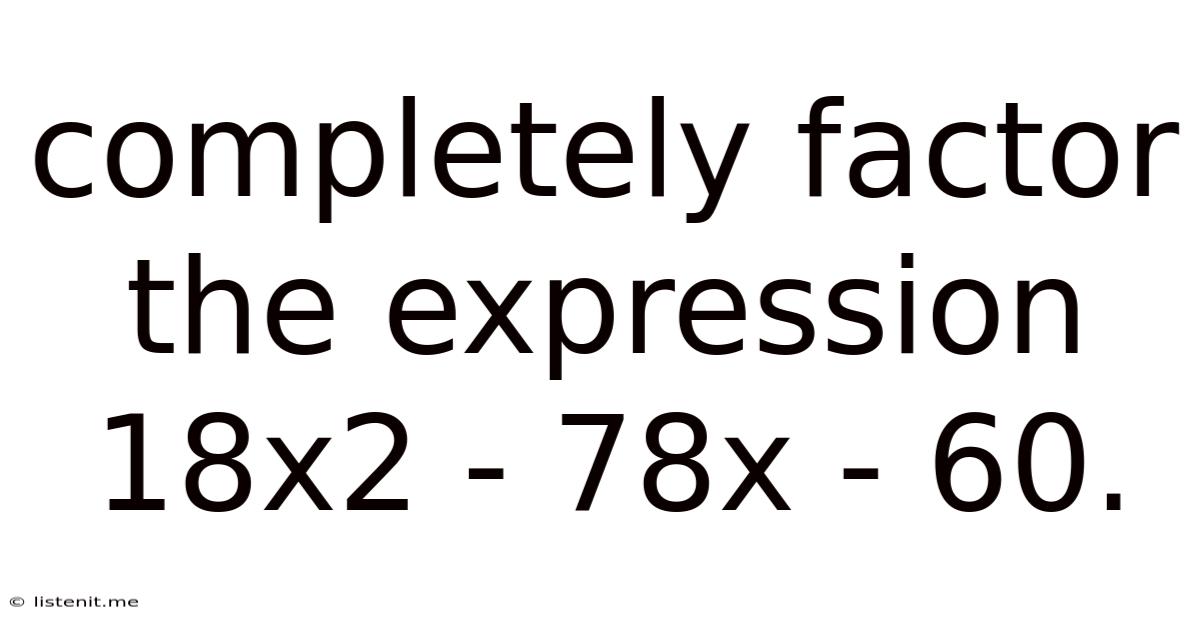
Table of Contents
Completely Factor the Expression 18x² - 78x - 60: A Comprehensive Guide
Factoring algebraic expressions is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding mathematical relationships. This article delves into the complete factorization of the quadratic expression 18x² - 78x - 60, providing a step-by-step approach, explaining the underlying principles, and offering various methods to achieve the solution. We’ll also explore common mistakes to avoid and discuss the importance of factoring in broader mathematical contexts.
Understanding Quadratic Expressions
Before diving into the factorization, let's establish a solid understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, 'x') is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants. Our expression, 18x² - 78x - 60, perfectly fits this mold, with a = 18, b = -78, and c = -60.
Step-by-Step Factorization: The Greatest Common Factor (GCF) Method
The first step in factoring any expression is to identify the greatest common factor (GCF) among all terms. This simplifies the expression and makes subsequent factorization easier. Let's analyze the coefficients: 18, -78, and -60.
The prime factorization of these numbers is:
- 18 = 2 x 3 x 3
- 78 = 2 x 3 x 13
- 60 = 2 x 2 x 3 x 5
The common factors are 2 and 3. Therefore, the GCF is 2 x 3 = 6. We can factor out this GCF from the original expression:
6(3x² - 13x - 10)
Factoring the Trinomial: 3x² - 13x - 10
Now we're left with a simpler trinomial: 3x² - 13x - 10. Factoring trinomials can be approached using several methods. Let's explore two common techniques:
Method 1: The AC Method
The AC method involves finding two numbers that add up to the coefficient of the 'x' term (-13) and multiply to the product of the coefficient of the x² term (3) and the constant term (-10), which is -30. These numbers are -15 and 2.
We rewrite the middle term (-13x) as the sum of these two numbers:
3x² - 15x + 2x - 10
Now we can factor by grouping:
3x(x - 5) + 2(x - 5)
Notice that (x - 5) is a common factor. We can factor it out:
(x - 5)(3x + 2)
Method 2: Trial and Error
This method involves directly trying different combinations of factors until we find the correct pair. Since the coefficient of x² is 3, the possible factors are (3x __)(x __). The constant term is -10, so we need to find factors of -10 that, when combined with the factors of 3x², produce the middle term -13x. After some trial and error, we find that (x - 5)(3x + 2) works.
Combining the Factors
Remember that we initially factored out a GCF of 6. Now that we've factored the trinomial, we can combine the factors to get the complete factorization of the original expression:
6(x - 5)(3x + 2)
Verification: Expanding the Factored Expression
To ensure our factorization is correct, let's expand the factored expression and see if we obtain the original expression:
6(x - 5)(3x + 2) = 6(3x² + 2x - 15x - 10) = 6(3x² - 13x - 10) = 18x² - 78x - 60
This confirms that our factorization is accurate.
Common Mistakes to Avoid
When factoring quadratic expressions, several common mistakes can occur:
- Forgetting the GCF: Always check for a GCF before proceeding with other factorization methods. This simplifies the process and avoids potential errors.
- Incorrect Sign Combinations: Pay close attention to the signs when factoring trinomials. Incorrect sign combinations will lead to an incorrect factorization.
- Not Checking Your Work: Always expand the factored expression to verify that it matches the original expression.
The Significance of Factoring in Mathematics
Factoring is not just a standalone algebraic technique; it's a cornerstone of many advanced mathematical concepts:
- Solving Quadratic Equations: Factoring is a fundamental method for solving quadratic equations. By setting the factored expression equal to zero and applying the zero-product property, we can find the roots (solutions) of the equation.
- Simplifying Rational Expressions: Factoring is crucial for simplifying rational expressions (fractions with polynomials in the numerator and denominator). By factoring both the numerator and denominator, we can often cancel out common factors, simplifying the expression.
- Calculus: Factoring plays a vital role in calculus, particularly in differentiation and integration. Being able to factor expressions efficiently simplifies many calculus problems.
- Graphing Quadratic Functions: The factored form of a quadratic expression readily reveals the x-intercepts (roots) of the corresponding quadratic function, making it easier to graph the function.
Conclusion: Mastering Factorization Techniques
Mastering the art of factoring, particularly quadratic expressions, is a crucial skill for any student of mathematics. This article provides a thorough explanation of factoring the expression 18x² - 78x - 60, detailing various methods and emphasizing the importance of checking your work. By understanding the underlying principles and practicing different techniques, you can build a strong foundation for tackling more complex algebraic problems and succeeding in your mathematical endeavors. Remember to always look for the GCF first and to carefully check your work. With consistent practice, factoring will become second nature.
Latest Posts
Latest Posts
-
40 As A Decimal And Fraction
May 10, 2025
-
What Is The Major Difference Between Primary And Secondary Succession
May 10, 2025
-
The Lanthanides And Actinides Belong Between
May 10, 2025
-
Find A Coterminal Angle Between 0 And 360
May 10, 2025
-
Rank The Following Elements In Order Of Decreasing Atomic Radius
May 10, 2025
Related Post
Thank you for visiting our website which covers about Completely Factor The Expression 18x2 - 78x - 60. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.