Which Expression Is Equivalent To The Following Complex Fraction
listenit
Mar 28, 2025 · 5 min read
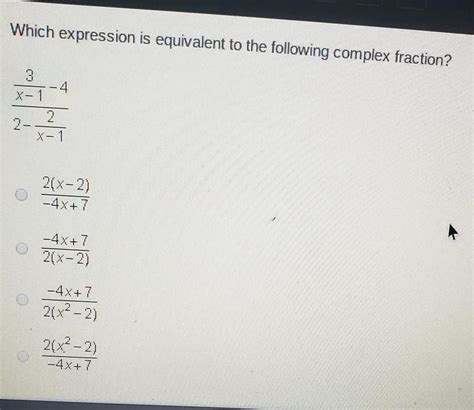
Table of Contents
Which Expression is Equivalent to the Following Complex Fraction? A Comprehensive Guide
Complex fractions can be intimidating, but mastering them unlocks a deeper understanding of rational expressions and algebraic manipulation. This article will delve into the intricacies of simplifying complex fractions, exploring various techniques and providing a comprehensive guide to determining equivalent expressions. We'll focus on identifying equivalent expressions, emphasizing the importance of understanding the underlying principles rather than just memorizing formulas.
Understanding Complex Fractions
A complex fraction is a fraction where either the numerator, the denominator, or both contain fractions themselves. For instance, (a/b) / (c/d) is a complex fraction. These fractions often appear daunting, but their simplification relies on fundamental principles of arithmetic and algebra. The key is to transform the complex fraction into a simpler, equivalent expression without fractions within fractions.
Methods for Simplifying Complex Fractions
There are primarily two methods for simplifying complex fractions:
Method 1: The "Invert and Multiply" Method
This is a popular method and often the most intuitive. It's based on the principle that dividing by a fraction is the same as multiplying by its reciprocal.
Steps:
- Identify the main fraction: Determine the numerator and denominator of the overall complex fraction.
- Simplify individual fractions: If possible, simplify any fractions within the numerator and denominator separately.
- Invert the denominator: Take the reciprocal of the fraction in the denominator.
- Multiply: Multiply the numerator by the inverted denominator.
- Simplify: Simplify the resulting expression by canceling common factors in the numerator and denominator.
Example:
Simplify the complex fraction: ( (2/3) + (1/2) ) / ( (3/4) - (1/2) )
- Simplify individual fractions: The numerator becomes
(4/6) + (3/6) = 7/6. The denominator becomes(3/4) - (2/4) = 1/4. - Rewrite as a single fraction: The complex fraction is now
(7/6) / (1/4). - Invert and multiply: This becomes
(7/6) * (4/1) = 28/6. - Simplify: Simplifying the fraction gives
14/3.
Therefore, the equivalent expression to the given complex fraction is 14/3.
Method 2: The "Find a Common Denominator" Method
This method is particularly useful when the numerator and denominator of the complex fraction are sums or differences of fractions.
Steps:
- Find a common denominator: For both the numerator and denominator, determine the least common denominator (LCD) of all the fractions involved.
- Rewrite fractions with common denominators: Rewrite all fractions within the numerator and denominator using the LCD.
- Simplify: Simplify the resulting fractions within the numerator and denominator.
- Divide: Divide the simplified numerator by the simplified denominator.
Example:
Let's use the same example as before: ( (2/3) + (1/2) ) / ( (3/4) - (1/2) )
- Find common denominators: The LCD for the numerator is 6, and the LCD for the denominator is 4.
- Rewrite with common denominators: The numerator becomes
(4/6) + (3/6) = 7/6. The denominator becomes(3/4) - (2/4) = 1/4. - The fraction becomes:
(7/6) / (1/4) - Divide: Dividing fractions is the same as multiplying by the reciprocal:
(7/6) * (4/1) = 28/6 = 14/3.
Again, we arrive at the equivalent expression 14/3.
Choosing the Right Method
Both methods are equally valid and will always lead to the same simplified expression. The choice often depends on personal preference and the specific form of the complex fraction. The "invert and multiply" method is often quicker and more straightforward for simple complex fractions, while the "common denominator" method can be more efficient when dealing with more complex sums or differences within the numerator and denominator.
Complex Fractions with Variables
The same principles apply when simplifying complex fractions involving variables. The key is to treat the variables as you would any number, following the same steps for simplification.
Example:
Simplify: ( (x/y) + 1 ) / ( (x/y) - 2 )
- Rewrite 1 and 2 as fractions:
( (x/y) + (y/y) ) / ( (x/y) - (2y/y) ) - Combine the fractions:
( (x+y)/y ) / ( (x-2y)/y ) - Invert and multiply:
( (x+y)/y ) * ( y/(x-2y) ) - Simplify:
(x+y) / (x-2y)
The equivalent expression is (x+y) / (x-2y).
Advanced Techniques and Considerations
Sometimes, simplifying a complex fraction might involve factoring, expanding, or other algebraic manipulations to identify common factors for cancellation. Always look for opportunities to simplify before applying either of the primary methods outlined above. Furthermore, remember that you must always be mindful of restrictions on the variables, particularly avoiding division by zero. For example, in the previous example, x cannot equal 2y as that would make the denominator zero.
Practical Applications of Complex Fractions
Complex fractions aren't merely abstract mathematical exercises; they appear frequently in various fields:
- Physics: Many physics equations involve ratios of rates or other quantities, leading to complex fractions.
- Engineering: Calculating circuit impedance or analyzing mechanical systems often involves simplifying complex fractions.
- Calculus: Derivatives and integrals frequently lead to expressions requiring simplification of complex fractions.
- Finance: Compound interest calculations or analyzing financial ratios can involve complex fractions.
Troubleshooting Common Errors
- Incorrectly inverting the denominator: Make sure to invert the entire denominator, not just part of it.
- Forgetting to simplify: Always simplify the resulting expression after inverting and multiplying or finding a common denominator.
- Ignoring restrictions on variables: Always be mindful of values that would lead to division by zero.
- Arithmetic errors: Double-check your calculations to avoid simple mistakes.
Conclusion
Simplifying complex fractions is a fundamental skill in algebra and related fields. By mastering both the "invert and multiply" and "common denominator" methods, you'll gain confidence in tackling these seemingly complex expressions. Remember to prioritize careful steps, thorough simplification, and awareness of potential pitfalls to arrive at accurate and equivalent expressions. Consistent practice is key to building fluency and achieving proficiency in simplifying complex fractions. Through understanding the underlying principles and applying the methods discussed here, you can effectively navigate the complexities of these expressions and unlock a deeper appreciation for their application across various disciplines. Remember to always check your work and ensure that your simplified expression is equivalent to the original complex fraction.
Latest Posts
Latest Posts
-
Finding The Radius Of A Circle From The Circumference
Mar 31, 2025
-
In Which Layer Does Weather Occur
Mar 31, 2025
-
What Is The Opposite Of 9
Mar 31, 2025
-
How Many Neutrons Does Carbon 13 Have
Mar 31, 2025
-
How Do You Find The Mass Of A Cube
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Which Expression Is Equivalent To The Following Complex Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
