Finding The Radius Of A Circle From The Circumference
listenit
Mar 31, 2025 · 5 min read
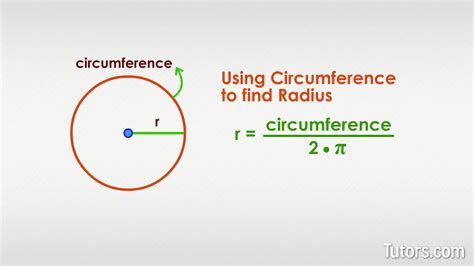
Table of Contents
Finding the Radius of a Circle from its Circumference: A Comprehensive Guide
Determining the radius of a circle given its circumference is a fundamental concept in geometry with wide-ranging applications in various fields. This comprehensive guide delves into the mathematical principles, practical applications, and problem-solving techniques associated with this crucial calculation. We'll explore different approaches, offering a detailed understanding suitable for students, professionals, and anyone curious about the fascinating world of circles.
Understanding the Relationship Between Circumference and Radius
The circumference (C) of a circle is the distance around its edge. The radius (r) is the distance from the center of the circle to any point on the circumference. These two measurements are intrinsically linked through a fundamental mathematical constant: π (pi). The formula expressing this relationship is:
C = 2πr
This equation tells us that the circumference is always equal to twice the radius multiplied by pi. Understanding this formula is the cornerstone of calculating the radius from the circumference.
Calculating the Radius: The Core Formula
To find the radius (r) when you know the circumference (C), we simply rearrange the fundamental formula:
r = C / 2π
This formula provides a direct method for calculating the radius. All you need is the value of the circumference and a reasonably accurate value for π (typically 3.14159 or the value provided by your calculator).
Step-by-Step Calculation:
Let's illustrate the process with an example:
Suppose a circle has a circumference of 25 centimeters. To find its radius:
- Write down the formula: r = C / 2π
- Substitute the known values: r = 25 cm / (2 * π)
- Calculate: Using π ≈ 3.14159, we get: r ≈ 25 cm / (2 * 3.14159) ≈ 25 cm / 6.28318 ≈ 3.98 cm
Therefore, the radius of the circle is approximately 3.98 centimeters.
Variations and Applications: Beyond the Basic Formula
While the core formula provides a straightforward method, understanding its applications and variations expands its usefulness in diverse contexts.
1. Working with Different Units:
The formula works seamlessly regardless of the units used for the circumference. Whether it's centimeters, meters, inches, feet, or any other unit of length, the resulting radius will be in the same unit. Consistency in units is crucial for accurate calculations.
2. Circumference Given Indirectly:
Sometimes, the circumference might not be explicitly provided. Instead, you might be given information that allows you to calculate the circumference. For example:
-
Diameter: The diameter (d) of a circle is twice its radius (d = 2r). If the diameter is known, the circumference can be calculated as C = πd, and subsequently, the radius can be found using r = C/2π or directly as r = d/2.
-
Area: The area (A) of a circle is given by A = πr². While this formula doesn't directly give the circumference, it provides a pathway. Solving for 'r' in the area formula (r = √(A/π)) gives the radius, from which the circumference can be calculated (C = 2πr).
-
Arc Length and Central Angle: If you know the length of an arc (s) and the measure of its corresponding central angle (θ in radians), you can find the circumference. The formula is: C = (s/θ) * 2π. Once you have the circumference, you can apply the standard radius formula.
3. Real-World Applications:
The ability to determine a circle's radius from its circumference is crucial in numerous practical applications:
-
Engineering: Calculating the radius of pipes, gears, wheels, and other circular components is essential in mechanical engineering and design.
-
Construction: Determining the radius of curved structures like arches, domes, and circular foundations is critical for accurate construction.
-
Architecture: Designing circular features in buildings requires precise radius calculations for aesthetic appeal and structural integrity.
-
Astronomy: Estimating the size of celestial bodies based on observed circumferences helps astronomers understand their scale and composition.
-
Mapping and Surveying: Measuring distances and plotting coordinates often involves calculating radii of circular features in geographic surveys.
Advanced Considerations and Error Analysis
While the basic formula is straightforward, some advanced considerations can improve accuracy and understanding:
1. Precision of π:
The accuracy of the radius calculation depends heavily on the precision of the value used for π. Using a more precise value (e.g., 3.14159265359) will yield a more accurate result, especially when dealing with large circumferences. Scientific calculators and programming languages provide high-precision values for π.
2. Error Propagation:
If the circumference measurement itself contains an error (e.g., due to measurement limitations), this error will propagate to the calculated radius. Understanding error propagation helps assess the uncertainty associated with the calculated radius.
3. Numerical Methods:
For complex scenarios or situations involving iterative calculations, numerical methods like iterative approximation techniques might be employed to refine the radius calculation, especially when dealing with non-linear relationships.
Problem-Solving Strategies and Practice Problems
Let's solidify our understanding with some practice problems:
Problem 1: A circular garden has a circumference of 30 meters. What is its radius?
Solution: Using the formula r = C / 2π, we get r = 30 m / (2 * π) ≈ 4.77 meters.
Problem 2: A circular track has a diameter of 50 yards. What is its radius?
Solution: The radius is half the diameter, so the radius is 25 yards. Alternatively, you could calculate the circumference (C = πd = 50π yards) and then find the radius (r = C / 2π = 25 yards).
Problem 3: A circular pizza has an area of 100 square inches. What is its radius?
Solution: First, we find the radius using the area formula: r = √(A/π) = √(100/π) ≈ 5.64 inches. Then, we can calculate the circumference: C = 2πr ≈ 35.45 inches.
Problem 4: A circular Ferris wheel has an arc length of 15 feet for a central angle of 1 radian. What is the radius of the Ferris wheel?
Solution: First find the circumference: C = (s/θ) * 2π = (15 feet / 1 radian) * 2π = 30π feet. Then find the radius: r = C/2π = 15 feet.
These examples demonstrate the adaptability of the core formula and its application in diverse scenarios.
Conclusion
Finding the radius of a circle from its circumference is a fundamental geometric calculation with widespread applications. Mastering the core formula, understanding its variations, and practicing problem-solving techniques equip you with a valuable skill applicable across various disciplines. Remember that accuracy depends on the precision of the input values (especially π) and an understanding of potential error propagation. This comprehensive guide provides a solid foundation for tackling radius calculations confidently and effectively. Remember to always double-check your calculations and use appropriate units for consistent and accurate results.
Latest Posts
Latest Posts
-
How Many Strings Does The Cello Have
Apr 01, 2025
-
What Percent Of 50 Is 9
Apr 01, 2025
-
40 Is 60 Percent Of What Number
Apr 01, 2025
-
What Is The Conjugate Acid Of Hco3
Apr 01, 2025
-
Indicate A Condensed Structural Formula For The Following Compound
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Finding The Radius Of A Circle From The Circumference . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
