Whats The Square Root Of 69
listenit
Apr 02, 2025 · 5 min read
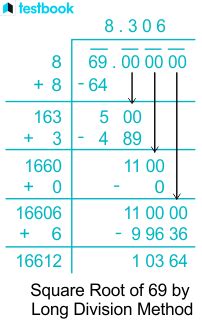
Table of Contents
What's the Square Root of 69? A Deep Dive into Square Roots and Beyond
The seemingly simple question, "What's the square root of 69?" opens a door to a fascinating exploration of mathematics, specifically the concept of square roots, their applications, and the broader world of numbers. While a calculator readily provides the approximate answer (8.3066), delving deeper reveals a rich tapestry of mathematical principles and practical uses. This article will not only answer the initial question but also explore the underlying concepts, providing a comprehensive understanding of square roots and their significance.
Understanding Square Roots
At its core, a square root is a number that, when multiplied by itself, equals a given number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. Similarly, the square root of 16 (√16) is 4 because 4 x 4 = 16. This relationship is fundamental to many areas of mathematics and science.
The Square Root of 69: An Approximation
The square root of 69 is not a whole number; it's an irrational number, meaning its decimal representation goes on forever without repeating. Using a calculator, we find that √69 ≈ 8.30662386292. This approximation is sufficient for most practical purposes, but it's crucial to understand why it's not a neat, whole number. Many numbers do not have perfect square roots, underscoring the complexity and beauty of the number system.
Methods for Calculating Square Roots
Before the advent of calculators, several methods existed for approximating square roots. These methods, while more laborious, provide a deeper understanding of the concept:
-
Babylonian Method (or Heron's Method): This iterative method refines an initial guess to progressively closer approximations. It's based on the formula: x_(n+1) = 0.5 * (x_n + S/x_n), where x_n is the current approximation, and S is the number whose square root we're seeking. By repeatedly applying this formula, we can obtain increasingly accurate approximations.
-
Binary Search Method: This method involves repeatedly narrowing down the interval within which the square root lies. By testing the midpoint of the interval and adjusting the boundaries accordingly, we converge toward the actual value.
-
Newton-Raphson Method: A more advanced iterative method used for finding the roots of equations, including square roots. It offers faster convergence than the Babylonian method.
Applications of Square Roots
The application of square roots extends far beyond simple mathematical exercises. They are essential tools in various fields:
Geometry and Trigonometry
-
Pythagorean Theorem: This fundamental theorem in geometry states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Calculating the length of a side often involves taking the square root. This has numerous applications in construction, surveying, and navigation.
-
Calculating Distances: In coordinate geometry, finding the distance between two points involves calculating the square root of the sum of the squares of the differences in their coordinates.
-
Circular Geometry: Calculating the radius or diameter of a circle given its area involves using the square root.
Physics and Engineering
-
Calculating Velocity: In physics, the square root is frequently used in formulas related to velocity, acceleration, and energy. For example, the velocity of an object under gravity is calculated using a formula involving a square root.
-
Electrical Engineering: Calculations involving impedance, reactance, and power often necessitate the use of square roots.
-
Structural Engineering: Stress calculations and analyses in structural engineering rely heavily on square root operations.
Statistics and Data Analysis
-
Standard Deviation: This crucial statistic, which measures the dispersion of data around the mean, involves calculating the square root of the variance. It's a cornerstone of statistical analysis.
-
Root Mean Square (RMS): Used extensively in signal processing and electrical engineering, RMS values provide a measure of the average magnitude of a fluctuating quantity.
Computer Graphics and Game Development
- 3D Transformations: Square roots play a crucial role in matrix operations used for rotating and scaling objects in 3D computer graphics and game development.
Beyond the Square Root of 69: Exploring Irrational Numbers
The square root of 69 belongs to the category of irrational numbers. Irrational numbers are numbers that cannot be expressed as a simple fraction (a ratio of two integers). They have infinite, non-repeating decimal expansions. Understanding irrational numbers is crucial for a complete grasp of the number system. Other famous irrational numbers include pi (π) and Euler's number (e).
The Significance of Irrational Numbers
The existence of irrational numbers profoundly impacted the development of mathematics. Their discovery challenged the ancient Greek belief that all numbers could be expressed as ratios of integers. The discovery of irrational numbers helped pave the way for more advanced mathematical concepts and theories.
Conclusion: The Broader Implications
The seemingly simple question about the square root of 69 leads us on a journey through the core concepts of mathematics, highlighting the importance and ubiquity of square roots in various fields. From the elegant geometry of the Pythagorean Theorem to the complex calculations in physics and engineering, the square root function is a fundamental tool. Furthermore, exploring the nature of irrational numbers opens our minds to the rich complexity and infinite beauty inherent within the number system. The answer itself, 8.3066 (approximately), is less significant than the understanding gained through exploring the broader mathematical landscape it reveals. It's a reminder of the interconnectedness of mathematical concepts and their practical applications in shaping our world.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 20 And 30
Apr 03, 2025
-
What Is The Square Root Of 170
Apr 03, 2025
-
How Long Does A Sensory Memory Last
Apr 03, 2025
-
63 Is 90 Percent Of What
Apr 03, 2025
-
A Square Is Always A Parallelogram
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Whats The Square Root Of 69 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
