A Square Is Always A Parallelogram
listenit
Apr 03, 2025 · 5 min read
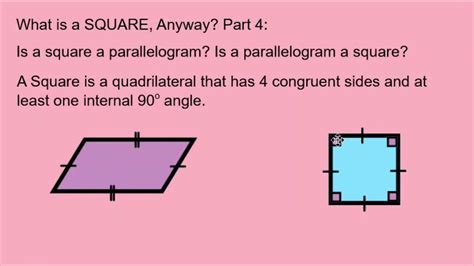
Table of Contents
A Square is Always a Parallelogram: A Comprehensive Exploration of Geometric Properties
This article delves into the fundamental relationship between squares and parallelograms, proving definitively that a square is always a parallelogram. We'll explore the defining characteristics of both shapes, analyze their properties, and demonstrate the logical connection between them. Understanding this relationship is crucial for mastering geometry and building a strong foundation in mathematics. We'll also touch upon related shapes and concepts to provide a holistic understanding.
Understanding the Definitions: Square and Parallelogram
Before we delve into the proof, let's clearly define the terms "square" and "parallelogram." This lays the groundwork for a rigorous and unambiguous demonstration.
What is a Square?
A square is a two-dimensional geometric shape defined by the following properties:
- Four sides: It possesses four straight sides of equal length.
- Four right angles: Each of its interior angles measures exactly 90 degrees.
- Opposite sides are parallel: The opposite sides are parallel to each other.
- Equal diagonals: Its two diagonals are equal in length and bisect each other at a 90-degree angle.
These properties collectively define a square, differentiating it from other quadrilaterals like rectangles, rhombuses, and trapezoids.
What is a Parallelogram?
A parallelogram is a quadrilateral (a four-sided polygon) characterized by:
- Opposite sides are parallel: This is the defining property of a parallelogram. The opposite sides are parallel to each other.
- Opposite sides are equal: The lengths of opposite sides are equal.
- Opposite angles are equal: The measures of opposite angles are equal.
- Consecutive angles are supplementary: Any two consecutive angles add up to 180 degrees.
- Diagonals bisect each other: The diagonals intersect at their midpoints.
Proving that a Square is a Parallelogram: A Step-by-Step Approach
The proof that a square is always a parallelogram is straightforward, relying directly on the defining properties of both shapes. We will use a deductive reasoning approach.
Premise: We start with the definition of a square: a quadrilateral with four equal sides and four right angles.
Step 1: Parallelism of Opposite Sides
A square, by definition, has four right angles. Consider any two opposite sides of the square. Because the angles between these sides and the adjacent sides are right angles (90 degrees), these opposite sides are parallel. This is a fundamental geometric principle: lines that are perpendicular to the same line are parallel to each other. Therefore, we can conclude that opposite sides of a square are parallel.
Step 2: Satisfying the Parallelogram Definition
The defining characteristic of a parallelogram is that its opposite sides are parallel. Since we've established that opposite sides of a square are parallel (Step 1), a square automatically satisfies the primary condition of being a parallelogram.
Conclusion:
Because a square fulfills the defining characteristic of a parallelogram (opposite sides are parallel), a square is always a parallelogram. This is a deductive logical conclusion directly derived from the properties of the square.
Expanding the Concept: Squares and Other Quadrilaterals
Understanding the square-parallelogram relationship helps clarify the hierarchy of quadrilaterals. Let's explore how squares relate to other shapes:
Square as a Special Case of a Rectangle
A rectangle is a parallelogram with four right angles. Since a square possesses four right angles and four equal sides (making its opposite sides equal and parallel), a square is a special case of a rectangle—a rectangle with all sides equal in length.
Square as a Special Case of a Rhombus
A rhombus is a parallelogram with four equal sides. A square fits this definition perfectly, possessing four equal sides and parallel opposite sides. Therefore, a square is also a special case of a rhombus—a rhombus with four right angles.
Summary of Quadrilateral Relationships
This hierarchy can be visualized as follows:
- Quadrilateral: The broadest category, encompassing all four-sided polygons.
- Parallelogram: Opposite sides are parallel.
- Rectangle: A parallelogram with four right angles.
- Rhombus: A parallelogram with four equal sides.
- Square: A parallelogram with four equal sides and four right angles (a special case of both a rectangle and a rhombus).
Real-World Applications: The Significance of Geometric Understanding
Understanding the properties of squares and parallelograms isn't just an academic exercise; it has numerous real-world applications:
- Architecture and Engineering: Squares and rectangles are fundamental to building design. The stability and structural integrity of buildings often rely on the properties of these shapes.
- Computer Graphics and Design: In digital design, squares and parallelograms are used extensively for creating shapes, defining spaces, and developing visual layouts. Understanding their properties allows for precise and efficient design.
- Manufacturing and Production: Many manufactured products are based on square and rectangular shapes due to their ease of production and efficiency in fitting together.
- Cartography and Geography: Squares and parallelograms are used in mapping and geographic information systems (GIS) to represent areas and locations.
Further Exploration: Advanced Geometric Concepts
For those interested in delving deeper into geometry, here are some related concepts to explore:
- Vectors: The properties of parallelograms can be elegantly expressed and proven using vector algebra.
- Coordinate Geometry: Representing squares and parallelograms on a coordinate plane allows for analytical solutions to various geometric problems.
- Transformations: Exploring geometric transformations like rotations, reflections, and translations on squares and parallelograms provides a deeper understanding of their properties.
- Tessellations: The ability of squares to tessellate (tile a plane without gaps or overlaps) is a crucial concept in various fields, including art and design.
Conclusion: The Inherent Connection Between Squares and Parallelograms
This comprehensive exploration has definitively proven that a square is always a parallelogram. This seemingly simple geometric relationship serves as a fundamental building block for understanding more complex geometric concepts. By carefully examining the defining properties of squares and parallelograms, we've demonstrated a clear logical connection, solidifying the understanding of these shapes within the broader context of geometry. The practical applications and further exploration avenues discussed highlight the real-world significance of this foundational geometric relationship, showcasing the power of mathematical reasoning and the interconnectedness of geometric concepts. Understanding this connection provides a solid basis for advancing to more advanced geometrical concepts and appreciating the elegance and utility of geometric principles.
Latest Posts
Latest Posts
-
What Energy Transformation Takes Place During Photosynthesis
Apr 04, 2025
-
What Does A Higher Specific Heat Mean
Apr 04, 2025
-
Question Plane Draw The Skeletal Structures
Apr 04, 2025
-
100 Yards On A Football Field
Apr 04, 2025
-
A Consumer That Eats Only Plants
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about A Square Is Always A Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
