63 Is 90 Percent Of What
listenit
Apr 03, 2025 · 4 min read
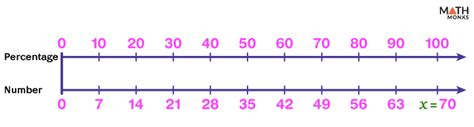
Table of Contents
63 is 90 Percent of What: A Comprehensive Guide to Percentage Calculations
Percentage calculations are fundamental to various aspects of life, from calculating discounts and taxes to understanding statistical data and financial reports. Knowing how to solve percentage problems efficiently is a crucial skill. This comprehensive guide will walk you through the process of determining what number 63 represents 90% of, and will equip you with the broader understanding of percentage calculations necessary for tackling similar problems.
Understanding Percentages
Before diving into the specifics of our problem ("63 is 90 percent of what"), let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100".
For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Similarly, 90% means 90 out of 100, or 90/100, or 0.9.
Method 1: Using Algebraic Equations
The most straightforward approach to solving "63 is 90% of what" is by setting up an algebraic equation. Let's represent the unknown number as 'x'. We can translate the problem into an equation as follows:
0.9x = 63
This equation states that 90% (or 0.9) of an unknown number (x) is equal to 63. To solve for x, we need to isolate it by dividing both sides of the equation by 0.9:
x = 63 / 0.9
Performing the division:
x = 70
Therefore, 63 is 90% of 70.
Method 2: Using the Percentage Formula
Another approach involves using the standard percentage formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 63 (the given value)
- Percentage: 90%
- Whole: x (the unknown value we want to find)
Plugging these values into the formula, we get:
(63 / x) * 100% = 90%
Now, we can solve for x:
- Divide both sides by 100%: 63/x = 0.9
- Multiply both sides by x: 63 = 0.9x
- Divide both sides by 0.9: x = 63 / 0.9
- Solve: x = 70
Again, we arrive at the solution: 63 is 90% of 70.
Method 3: Using Proportions
Proportions offer a visual and intuitive method to solve percentage problems. We can set up a proportion as follows:
63 / x = 90 / 100
This proportion states that the ratio of 63 to the unknown number (x) is equal to the ratio of 90 to 100 (representing 90%). To solve for x, we can cross-multiply:
63 * 100 = 90 * x
6300 = 90x
Now, divide both sides by 90:
x = 6300 / 90
x = 70
This method confirms our previous results: 63 is 90% of 70.
Practical Applications of Percentage Calculations
Understanding how to solve percentage problems is incredibly useful in numerous real-world scenarios. Here are a few examples:
1. Sales and Discounts:
Imagine a store offers a 90% discount on an item. If the discounted price is $63, you can use the methods described above to determine the original price. As we've seen, the original price was $70.
2. Financial Calculations:
Percentage calculations are essential for understanding interest rates, tax calculations, profit margins, and investment returns. For example, if you earn 90% of your projected income, you can use this knowledge to adjust your budget or savings accordingly.
3. Statistical Analysis:
Percentages are fundamental to interpreting data in various fields, such as healthcare, education, and market research. Understanding percentage changes helps in tracking trends, comparing groups, and making informed decisions.
4. Grade Calculations:
Percentage calculations are used extensively in educational settings. If you score 63 out of 70 points on a test, you've achieved a 90% grade.
Expanding Your Percentage Skills: Working with Different Percentages and Values
The principles we've used to solve "63 is 90% of what" can be applied to any percentage problem. Simply replace the numbers with the appropriate values, and follow the same steps.
For example, let's try a slightly different problem: "45 is 75% of what?"
Using the algebraic method:
0.75x = 45
x = 45 / 0.75
x = 60
Therefore, 45 is 75% of 60.
Troubleshooting Common Percentage Errors
While percentage calculations are relatively straightforward, some common errors can arise. Here are a few to watch out for:
- Incorrect Decimal Conversion: Always ensure you correctly convert percentages to decimals (e.g., 90% becomes 0.9) before performing calculations.
- Misplacing the Decimal Point: Double-check the placement of decimal points during division and multiplication steps.
- Calculation Errors: Carefully review your calculations to prevent simple arithmetic mistakes. Using a calculator can minimize the risk of errors.
Conclusion
Mastering percentage calculations is a valuable skill with wide-ranging applications. Whether dealing with discounts, financial reports, or statistical analysis, the ability to solve percentage problems confidently will significantly enhance your numerical literacy and problem-solving capabilities. This guide has provided a thorough understanding of how to tackle problems like "63 is 90% of what," showcasing multiple methods and offering practical examples. Remember to practice regularly, and you'll become proficient in navigating the world of percentages with ease.
Latest Posts
Latest Posts
-
100 Yards On A Football Field
Apr 04, 2025
-
A Consumer That Eats Only Plants
Apr 04, 2025
-
The Amount Of Energy Required To Raise The Temperature
Apr 04, 2025
-
38 Out Of 40 Is What Percent
Apr 04, 2025
-
Which Polynomial Represents The Sum Below
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 63 Is 90 Percent Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
