What's The Square Root Of 54
listenit
Mar 30, 2025 · 4 min read
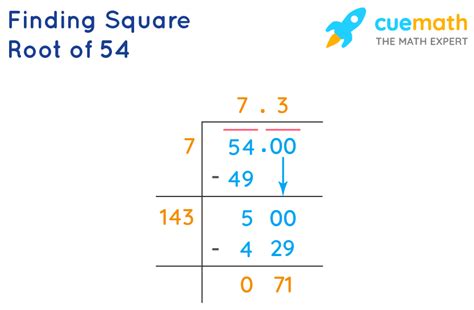
Table of Contents
What's the Square Root of 54? A Deep Dive into Square Roots and Approximation Techniques
The question, "What's the square root of 54?" seems simple enough. However, delving into this seemingly straightforward problem opens the door to a fascinating exploration of mathematical concepts, approximation techniques, and the power of iterative methods. Let's embark on this journey, moving from the basics of square roots to sophisticated methods for finding increasingly precise approximations.
Understanding Square Roots
Before we tackle the square root of 54, let's solidify our understanding of what a square root actually is. The square root of a number, 'x', is a value that, when multiplied by itself (squared), equals 'x'. In simpler terms, it's the inverse operation of squaring a number. For example:
- The square root of 9 (√9) is 3, because 3 * 3 = 9.
- The square root of 16 (√16) is 4, because 4 * 4 = 16.
Now, 54 isn't a perfect square – meaning there isn't a whole number that, when multiplied by itself, equals 54. This is where things get interesting. We need to explore methods to approximate the square root of 54.
Methods for Approximating √54
Several methods can approximate the square root of 54. Let's examine a few, ranging from simple estimation to more advanced iterative techniques:
1. Estimation through Perfect Squares
We can start by identifying perfect squares close to 54. We know that 7² = 49 and 8² = 64. Since 54 lies between 49 and 64, the square root of 54 must be between 7 and 8. This gives us a rough estimate, but it's not very precise.
2. Using a Calculator
The most straightforward method is to use a calculator. Most calculators have a dedicated square root function (√). Simply input 54 and press the square root button. You'll obtain a decimal approximation, typically around 7.348. This is a quick and easy method for obtaining a highly accurate result.
3. Babylonian Method (or Heron's Method)
This iterative method refines an initial guess to progressively closer approximations of the square root. The algorithm is as follows:
- Start with an initial guess: Let's use our earlier estimate of 7.
- Improve the guess: Divide the number (54) by the guess (7), and then average the result with the guess: (7 + 54/7) / 2 ≈ 7.357
- Repeat: Use the improved guess (7.357) as the new guess and repeat step 2. Each iteration brings the approximation closer to the actual square root.
Let's perform a few iterations:
- Iteration 1: (7 + 54/7) / 2 ≈ 7.357
- Iteration 2: (7.357 + 54/7.357) / 2 ≈ 7.348
- Iteration 3: (7.348 + 54/7.348) / 2 ≈ 7.348
Notice how quickly the method converges to a highly accurate result (7.348).
4. Newton-Raphson Method
This is another powerful iterative method often used for finding roots of equations, including square roots. It's similar to the Babylonian method but uses calculus concepts for faster convergence. The formula for finding the square root of 'x' using the Newton-Raphson method is:
x_(n+1) = 0.5 * (x_n + x/x_n)
Where:
- x_n is the current approximation.
- x_(n+1) is the next, improved approximation.
- x is the number for which we're finding the square root (54 in our case).
This method also converges rapidly to a highly accurate solution.
5. Logarithms and Exponents
The square root of a number can also be calculated using logarithms and exponents. The following relationship holds true:
√x = x^(1/2) = e^(0.5 * ln(x))
This approach requires familiarity with logarithms and exponential functions.
Understanding the Decimal Approximation: 7.348
The commonly cited approximation for √54 is 7.348. It's essential to understand that this is just an approximation. The actual value of √54 is an irrational number, meaning its decimal representation goes on forever without repeating. 7.348 is a truncated version, offering a level of precision suitable for many applications.
Practical Applications and Significance
Understanding how to calculate square roots, and particularly how to approximate them, has numerous applications across various fields:
- Engineering and Physics: Calculating distances, forces, and other quantities often involves square roots.
- Computer Graphics: Square roots are fundamental to many graphical calculations, including 2D and 3D transformations.
- Statistics: Standard deviation calculations frequently involve square roots.
- Mathematics: Square roots form the basis for many more advanced mathematical concepts.
Conclusion: More Than Just a Number
The seemingly simple question, "What's the square root of 54?", has led us on a journey exploring various mathematical concepts and approximation techniques. We've seen how different methods, ranging from simple estimation to sophisticated iterative approaches, can yield increasingly precise approximations. Understanding these methods is crucial not just for solving specific problems but also for appreciating the elegance and power of mathematics in general. The approximation, 7.348, while seemingly just a number, represents a culmination of mathematical ingenuity and the quest for precise solutions. Beyond the numerical answer itself lies a richer understanding of the underlying principles that govern the world of numbers and calculations.
Latest Posts
Latest Posts
-
How Many 1 3 Cups Equal 2 3 Cup
Apr 01, 2025
-
How To Find Complement And Supplement Of An Angle
Apr 01, 2025
-
What Is The Sum Of A And 8
Apr 01, 2025
-
Does Dry Ice Melt Or Evaporate
Apr 01, 2025
-
What Is The Common Factor Of 6 And 12
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
