How Many 1 3 Cups Equal 2 3 Cup
listenit
Apr 01, 2025 · 5 min read
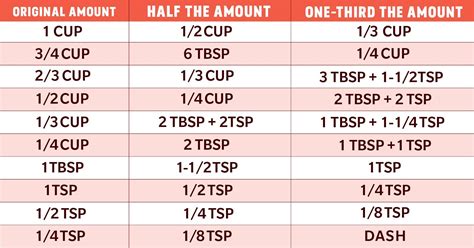
Table of Contents
How Many 1/3 Cups Equal 2/3 Cup? A Comprehensive Guide to Fraction Conversions
Understanding fractions is fundamental to baking, cooking, and various other aspects of life. This seemingly simple question – "How many 1/3 cups equal 2/3 cup?" – opens the door to a deeper understanding of fractional relationships and how to solve similar problems. This comprehensive guide will not only answer this question but also equip you with the knowledge and skills to tackle more complex fraction conversions.
Understanding Fractions: A Quick Refresher
Before diving into the specific problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In the context of our question, we're dealing with thirds (denominator = 3). A 1/3 cup represents one part out of three equal parts of a whole cup, while a 2/3 cup represents two parts out of three equal parts.
Solving the Problem: How Many 1/3 Cups Equal 2/3 Cup?
The question, "How many 1/3 cups equal 2/3 cup?" can be solved in a few different ways:
Method 1: Visual Representation
Imagine a cup divided into three equal sections. Each section represents 1/3 of a cup. To get 2/3 of a cup, you need to fill two of these sections. Therefore, two 1/3 cups equal 2/3 cup.
Method 2: Simple Arithmetic
This is the most straightforward method. We can represent the problem as an equation:
x * (1/3) = 2/3
To solve for x (the number of 1/3 cups), we simply divide both sides of the equation by 1/3:
x = (2/3) / (1/3)
Remember that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 1/3 is 3/1 or simply 3. So the equation becomes:
x = (2/3) * 3
x = 6/3
x = 2
Therefore, two 1/3 cups equal 2/3 cup.
Method 3: Understanding Equivalent Fractions
Another approach involves finding equivalent fractions. We want to know how many 1/3 cups make up 2/3 cups. We can think about this in terms of finding an equivalent fraction with a numerator of 2.
To do this, we can multiply the numerator and denominator of 1/3 by the same number to find a fraction equivalent to 2/3. If we multiply both the numerator and denominator of 1/3 by 2, we get:
(1 * 2) / (3 * 2) = 2/6
This isn't directly helpful. Instead we are looking for how many 1/3 make up 2/3. We can look at it this way:
2/3 = 1/3 + 1/3
This visually shows that two 1/3 cups combine to make 2/3 of a cup.
Expanding the Understanding: Working with Different Fractions
The principles discussed above can be applied to other fractional conversions. Let's explore a few examples:
Example 1: How many 1/4 cups equal 1/2 cup?
- Method 1 (Visual): Imagine a cup divided into four equal sections. Each section is 1/4 cup. To get 1/2 cup, you need two of these sections (because 1/2 = 2/4).
- Method 2 (Arithmetic): x * (1/4) = 1/2 => x = (1/2) / (1/4) = (1/2) * 4 = 2
- Answer: Two 1/4 cups equal 1/2 cup.
Example 2: How many 1/8 cups equal 3/4 cup?
- Method 1 (Visual): A cup is divided into eight equal sections (1/8 cup each). 3/4 cup is equivalent to 6/8 cup (because 3/4 = 6/8). You would need six 1/8 cup sections.
- Method 2 (Arithmetic): x * (1/8) = 3/4 => x = (3/4) / (1/8) = (3/4) * 8 = 24/4 = 6
- Answer: Six 1/8 cups equal 3/4 cup.
Practical Applications: Baking and Cooking
Understanding fraction conversions is crucial in baking and cooking, where precise measurements are essential for successful results. Incorrect measurements can significantly impact the taste and texture of your dishes. Consider these scenarios:
-
Baking a cake: A recipe calls for 2/3 cup of sugar, but you only have a 1/3 cup measuring cup. You now know you need to use the 1/3 cup measure twice.
-
Cooking a sauce: A recipe requires 1/2 cup of broth, but you only have a 1/4 cup measuring cup. You'll need to use the 1/4 cup measuring cup twice.
-
Adjusting recipes: Perhaps you want to halve a recipe. Understanding fractions allows you to accurately adjust the ingredient quantities.
Beyond the Kitchen: Real-World Applications
Fractions aren't limited to the kitchen. They're prevalent in various aspects of daily life, including:
- Construction and Engineering: Measuring materials and calculating dimensions.
- Finance: Calculating interest rates, proportions, and percentages.
- Data Analysis: Representing parts of a whole in statistical data.
- Map Reading: Understanding scales and distances.
Mastering Fractions: Tips and Resources
Mastering fractions takes practice. Here are some tips:
- Visual Aids: Use visual aids like diagrams or physical objects to visualize fractions.
- Practice Problems: Solve various fraction problems to build confidence and understanding.
- Online Resources: Explore online resources like educational websites or apps that offer interactive fraction exercises.
- Real-World Applications: Apply your knowledge of fractions to real-world situations, such as cooking or budgeting.
Conclusion: Embracing the Power of Fractions
The simple question of "How many 1/3 cups equal 2/3 cup?" serves as a gateway to a broader understanding of fractions and their practical applications. By mastering fractional conversions, you enhance your problem-solving skills and unlock the ability to tackle more complex mathematical challenges in various fields. Remember, consistent practice and a willingness to explore different methods will solidify your understanding and build confidence in your ability to work with fractions. So, next time you encounter a fractional measurement, you'll be ready to tackle it with confidence and precision.
Latest Posts
Latest Posts
-
What Is 5 9 In Decimal Form
Apr 02, 2025
-
How Many Grams In 8 Kilograms
Apr 02, 2025
-
12x 4y 20 Solve For Y
Apr 02, 2025
-
Most Reactive Group On The Periodic Table
Apr 02, 2025
-
How To Solve Multi Step Inequalities
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How Many 1 3 Cups Equal 2 3 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
