How To Find Complement And Supplement Of An Angle
listenit
Apr 01, 2025 · 5 min read
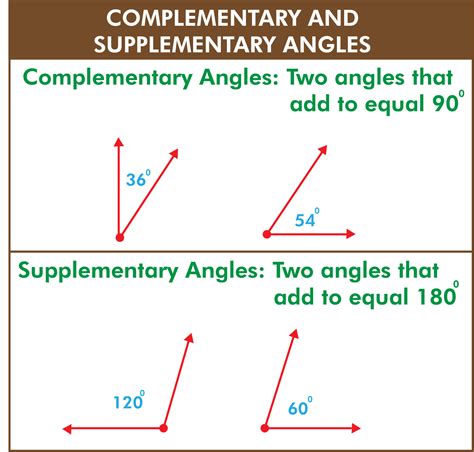
Table of Contents
How to Find the Complement and Supplement of an Angle: A Comprehensive Guide
Understanding complementary and supplementary angles is fundamental in geometry and trigonometry. These concepts form the bedrock for solving numerous problems involving angles and their relationships within shapes and figures. This comprehensive guide will delve deep into the definitions, calculations, and practical applications of finding the complement and supplement of an angle. We'll cover various scenarios, including those involving algebraic expressions, and provide ample examples to solidify your understanding.
What are Complementary Angles?
Two angles are considered complementary if their sum equals 90 degrees (or π/2 radians). Think of it like completing a right angle – the two angles "complement" each other to form a right angle.
Key Characteristics:
- Sum: The sum of complementary angles is always 90 degrees.
- Types: Complementary angles can be both acute (less than 90 degrees) or a combination of acute angles. They cannot be obtuse (greater than 90 degrees).
- Relationship: They are often found adjacent to each other (sharing a common side) to form a right angle. However, they don't need to be adjacent; any two angles that add up to 90 degrees are complementary.
Example 1: Finding the Complement
Let's say we have an angle of 35 degrees. To find its complement, we subtract the angle from 90 degrees:
90° - 35° = 55°
Therefore, the complement of 35 degrees is 55 degrees.
Example 2: Finding an Angle Given its Complement
Suppose you know that an angle's complement is 20 degrees. To find the angle itself:
90° - 20° = 70°
The angle is 70 degrees.
Example 3: Complementary Angles with Algebraic Expressions
Let's consider a scenario where one angle is represented by 'x' and its complement is represented by '2x + 10'. We can set up an equation:
x + (2x + 10) = 90
Solving for x:
3x + 10 = 90 3x = 80 x = 80/3
Therefore, one angle is 80/3 degrees, and its complement is 2(80/3) + 10 = 190/3 degrees. Always check that the sum of the angles is 90 degrees.
What are Supplementary Angles?
Two angles are considered supplementary if their sum equals 180 degrees (or π radians). Imagine a straight line – supplementary angles "supplement" each other to form a straight line.
Key Characteristics:
- Sum: The sum of supplementary angles is always 180 degrees.
- Types: Supplementary angles can be a combination of acute and obtuse angles, or even two right angles.
- Relationship: Often, they are adjacent and form a linear pair (a pair of angles on a straight line). But like complementary angles, they don't have to be adjacent; any two angles that sum to 180 degrees are supplementary.
Example 4: Finding the Supplement
If we have an angle of 110 degrees, its supplement is:
180° - 110° = 70°
The supplement of 110 degrees is 70 degrees.
Example 5: Finding an Angle Given its Supplement
If the supplement of an angle is 45 degrees, the angle itself is:
180° - 45° = 135°
Example 6: Supplementary Angles with Algebraic Expressions
Consider two angles represented by 'y' and '3y - 20'. Their supplementary relationship can be expressed as:
y + (3y - 20) = 180
Solving for y:
4y - 20 = 180 4y = 200 y = 50
Therefore, one angle is 50 degrees, and its supplement is 3(50) - 20 = 130 degrees. Again, verify that their sum is 180 degrees.
Solving Problems with Complementary and Supplementary Angles
Many geometry problems involve finding missing angles using the principles of complementary and supplementary angles. Let's explore a few examples:
Problem 1: Two angles are complementary. One angle is twice the size of the other. Find the measure of each angle.
Let's denote the smaller angle as 'x'. The larger angle is '2x'. Since they are complementary, their sum is 90 degrees:
x + 2x = 90 3x = 90 x = 30
The smaller angle is 30 degrees, and the larger angle is 2 * 30 = 60 degrees.
Problem 2: Angles A and B are supplementary. Angle A is 30 degrees more than twice the measure of Angle B. Find the measure of each angle.
Let Angle B be 'x'. Angle A is '2x + 30'. Since they are supplementary:
x + (2x + 30) = 180 3x + 30 = 180 3x = 150 x = 50
Angle B is 50 degrees, and Angle A is 2(50) + 30 = 130 degrees.
Problem 3: Angles in a Triangle
Remember that the sum of angles in any triangle is always 180 degrees. This concept often intertwines with complementary and supplementary angles. Let's say a triangle has angles of x, 2x, and 3x. We can solve for x:
x + 2x + 3x = 180 6x = 180 x = 30
The angles are 30 degrees, 60 degrees, and 90 degrees (a right-angled triangle). Notice that the 60-degree and 30-degree angles are complementary.
Advanced Applications and Considerations
The concepts of complementary and supplementary angles extend beyond basic geometry. They are crucial in:
- Trigonometry: Many trigonometric identities and formulas rely on understanding the relationships between complementary and supplementary angles.
- Vector Analysis: The angles between vectors are often analyzed in terms of their complements and supplements.
- Computer Graphics: Understanding angles and their relationships is essential in computer graphics programming for tasks like rotations and transformations.
- Engineering and Physics: Numerous applications in engineering and physics involve the calculations of angles, often leveraging the properties of complementary and supplementary angles.
Troubleshooting Common Mistakes
- Mixing up complements and supplements: Remember that complements add up to 90 degrees, while supplements add up to 180 degrees. Clearly define which type of angle relationship you're working with.
- Incorrect algebraic manipulation: Double-check your algebraic steps when solving equations involving angles. A simple mistake can lead to an incorrect answer.
- Failing to check your answer: Always verify that your solution makes sense in the context of the problem. Do the angles add up to the correct sum (90 or 180 degrees)? Are the angles realistic within the given geometrical context?
By understanding the fundamental definitions, practicing with examples, and carefully reviewing your calculations, you'll master the skills to confidently find the complements and supplements of any angle. This knowledge forms a strong foundation for further explorations in geometry and related fields. Remember that consistent practice is key to solidifying these concepts. Work through various problems, experiment with different angle values, and don't hesitate to review the explanations provided in this guide when needed. The journey to mastering these concepts is a rewarding one, paving the way for success in more advanced mathematical pursuits.
Latest Posts
Latest Posts
-
How Many Kilograms Are In 5000 Grams
Apr 02, 2025
-
Solve This Inequality 3b 7 32
Apr 02, 2025
-
Number Of Valence Electrons In Ar
Apr 02, 2025
-
What Is 5 9 In Decimal Form
Apr 02, 2025
-
How Many Grams In 8 Kilograms
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How To Find Complement And Supplement Of An Angle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
