Whats The Square Root Of 289
listenit
Apr 04, 2025 · 5 min read
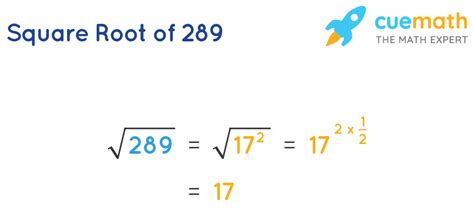
Table of Contents
What's the Square Root of 289? A Deep Dive into Square Roots and Their Applications
The seemingly simple question, "What's the square root of 289?" opens a door to a fascinating world of mathematics, encompassing concepts that extend far beyond basic arithmetic. This article will not only answer that question definitively but also explore the broader meaning of square roots, their properties, methods for calculating them, and their practical applications in various fields.
Understanding Square Roots: The Basics
A square root of a number is a value that, when multiplied by itself, gives the original number. In simpler terms, it's the inverse operation of squaring a number. For example, the square root of 9 (written as √9) is 3 because 3 x 3 = 9. Similarly, the square root of 16 (√16) is 4 because 4 x 4 = 16.
Key Terminology:
- Radicand: The number under the square root symbol (√). In √289, 289 is the radicand.
- Radical: The symbol itself (√) indicating the square root operation.
- Principal Square Root: Every positive number has two square roots – one positive and one negative. The principal square root is the non-negative square root. For example, while both 3 and -3 are square roots of 9, the principal square root is 3.
Calculating the Square Root of 289: Methods and Approaches
There are several ways to determine the square root of 289:
1. Prime Factorization: A Fundamental Approach
Prime factorization involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves). This method can be particularly useful for larger numbers or when dealing with perfect squares.
Let's factorize 289:
- 289 is not divisible by 2 (it's odd).
- 289 is not divisible by 3 (the sum of its digits, 2+8+9=19, is not divisible by 3).
- 289 is not divisible by 5 (it doesn't end in 0 or 5).
- 289 is not divisible by 7 (289 ÷ 7 ≈ 41.28).
- 289 is not divisible by 11 (289 ÷ 11 ≈ 26.27).
- 289 is not divisible by 13 (289 ÷ 13 ≈ 22.23).
- However, 17 x 17 = 289.
Therefore, the prime factorization of 289 is 17². This directly tells us that the square root of 289 is 17.
2. Using a Calculator: The Quickest Method
The simplest and most efficient way to find the square root of 289 is by using a calculator. Most calculators have a dedicated square root function (usually denoted as √ or √x). Simply enter 289 and press the square root button to obtain the answer: 17.
3. Estimation and Iteration (Newton's Method): A Numerical Approach
For numbers that aren't easily recognized as perfect squares, iterative methods like Newton's method can be employed. This involves making an initial guess and refining it through successive iterations. While not necessary for 289 (as its square root is easily identifiable), understanding the concept is valuable for larger or non-perfect squares.
Newton's method for finding the square root of a number 'x' involves the iterative formula:
x_(n+1) = 0.5 * (x_n + x/x_n)
Where:
- x_n is the current estimate.
- x_(n+1) is the improved estimate.
Let's illustrate this with a slightly different example (finding √25):
- Initial Guess: Let's start with x_0 = 5.
- Iteration 1: x_1 = 0.5 * (5 + 25/5) = 5 (already accurate!)
This method converges quickly to the correct solution, especially if the initial guess is close to the actual square root.
The Significance of Square Roots in Mathematics and Beyond
Square roots are fundamental building blocks in various mathematical concepts and have wide-ranging practical applications:
1. Geometry and Trigonometry: Calculating Distances and Areas
Square roots are crucial in calculating distances and areas using the Pythagorean theorem. This theorem states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides (a² + b² = c²). Solving for the length of a side often involves taking the square root. This is essential in surveying, construction, and computer graphics.
2. Physics and Engineering: Solving Equations and Modeling Phenomena
Numerous physics and engineering equations involve square roots. For example, calculating the velocity of an object involves square roots in the context of kinetic energy (KE = 1/2mv²) or the speed of sound in different mediums. They are crucial in fields like mechanics, electronics, and fluid dynamics.
3. Statistics and Data Analysis: Standard Deviation and Error Calculations
Square roots play a significant role in statistics when calculating standard deviations and errors. The standard deviation measures the spread or dispersion of a data set, crucial for understanding data variability and reliability. This is used extensively in research, finance, and market analysis.
4. Computer Science and Programming: Algorithms and Numerical Computations
Square roots are frequently used in computer algorithms and numerical computations. Efficient algorithms are designed to calculate square roots quickly and accurately, fundamental for applications ranging from game development (calculating distances between objects) to scientific simulations (modeling physical phenomena).
5. Number Theory: Exploring Perfect Squares and Diophantine Equations
In number theory, square roots are central to understanding perfect squares, numbers that are the square of an integer. Moreover, they're used extensively in solving Diophantine equations, equations involving integer solutions.
Beyond the Square Root of 289: Exploring Higher-Order Roots
While this article primarily focuses on square roots, it's worth mentioning higher-order roots like cube roots (∛), fourth roots (∜), and so on. These roots represent the inverse operations of raising a number to the corresponding power. For instance, the cube root of 8 (∛8) is 2 because 2 x 2 x 2 = 8. These higher-order roots also find applications in various fields, especially in advanced mathematics and scientific modeling.
Conclusion: The Power of a Simple Question
The seemingly simple question, "What's the square root of 289?" has led us on a journey through the world of mathematics, revealing the significance and far-reaching applications of square roots. From basic calculations to advanced mathematical concepts and practical applications in various fields, understanding square roots is essential for anyone seeking a deeper comprehension of mathematics and its impact on our world. The answer, 17, is merely the starting point of a much larger and more intricate mathematical landscape.
Latest Posts
Latest Posts
-
How Do You Find Ml Quantum Number
Apr 04, 2025
-
How Many Unpaired Electrons Does Manganese Have
Apr 04, 2025
-
Water Is Made Up Of Which Two Elements
Apr 04, 2025
-
What Is 9 Percent Of 50
Apr 04, 2025
-
Distance From Earth To Pluto In Light Years
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Whats The Square Root Of 289 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
