What's Half Of 1 And 1/4
listenit
May 09, 2025 · 4 min read
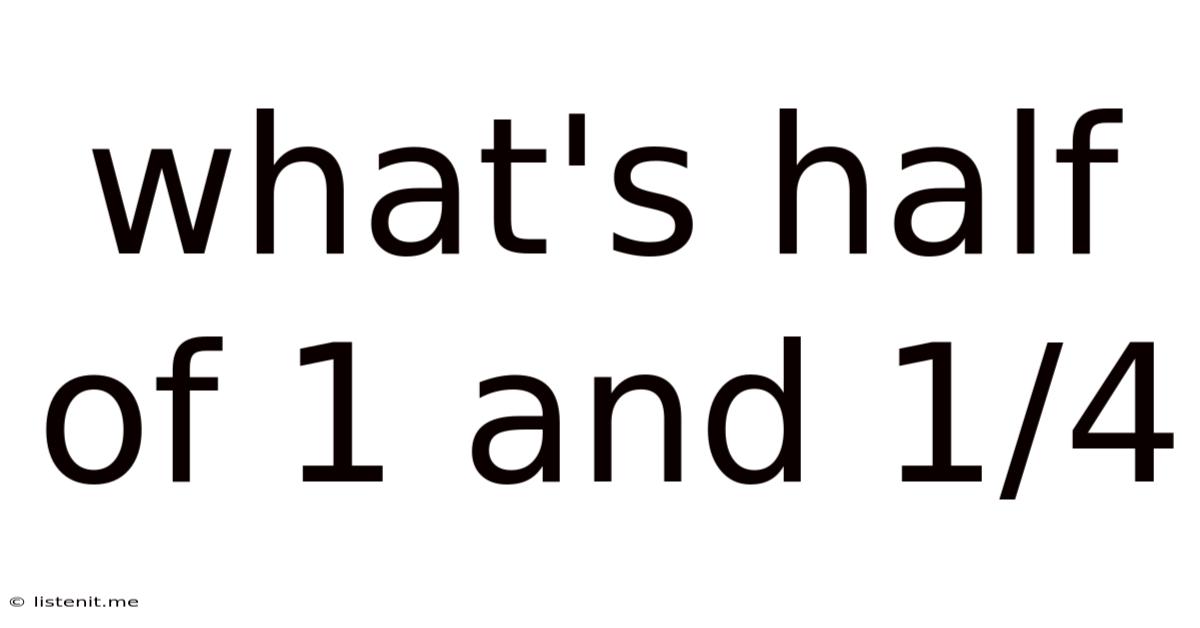
Table of Contents
What's Half of 1 and 1/4? A Deep Dive into Fractions and Problem-Solving
Finding half of any number is a fundamental mathematical operation, crucial for various applications from everyday tasks to complex calculations. This article will explore how to calculate half of 1 and 1/4, providing a comprehensive understanding of the process, its variations, and related concepts. We'll delve into the intricacies of fraction manipulation, demonstrating multiple methods to arrive at the correct solution. Furthermore, we’ll discuss the broader implications of this seemingly simple calculation and its relevance in real-world scenarios.
Understanding Fractions: A Refresher
Before tackling the core problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For instance, in the fraction 1/4, 1 is the numerator and 4 is the denominator, signifying one part out of four equal parts.
Converting Mixed Numbers to Improper Fractions
The number "1 and 1/4" is a mixed number, combining a whole number (1) and a fraction (1/4). To perform calculations more easily, it's often beneficial to convert mixed numbers into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
To convert 1 and 1/4 to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 1 * 4 = 4
- Add the numerator to the result: 4 + 1 = 5
- Keep the same denominator: 4
Therefore, 1 and 1/4 is equivalent to the improper fraction 5/4.
Calculating Half of 1 and 1/4: Method 1 (Using Improper Fractions)
Now that we've converted 1 and 1/4 to 5/4, finding half is a simple matter of division. To find half of a number, we divide it by 2 (or multiply it by 1/2).
-
Express the problem mathematically: (5/4) / 2 or (5/4) * (1/2)
-
Multiply the numerators together: 5 * 1 = 5
-
Multiply the denominators together: 4 * 2 = 8
-
The result is: 5/8
Therefore, half of 1 and 1/4 is 5/8.
Calculating Half of 1 and 1/4: Method 2 (Working with Mixed Numbers)
While converting to an improper fraction is often the most efficient method, we can also work directly with the mixed number.
-
Find half of the whole number: Half of 1 is 1/2
-
Find half of the fraction: Half of 1/4 is (1/4) / 2 = 1/8
-
Add the two halves together: 1/2 + 1/8
To add these fractions, we need a common denominator, which is 8. We convert 1/2 to an equivalent fraction with a denominator of 8: (1/2) * (4/4) = 4/8
- Add the fractions: 4/8 + 1/8 = 5/8
Again, we arrive at the answer: 5/8.
Real-World Applications: Where This Calculation Matters
This seemingly simple calculation has numerous practical applications in everyday life:
-
Cooking and Baking: Recipes often require halving or doubling ingredients. Understanding fractions is vital for accurate measurements and consistent results. Imagine needing to halve a recipe that calls for 1 and 1/4 cups of flour – this calculation is key.
-
Construction and Engineering: Precision is paramount in construction and engineering projects. Calculations involving fractions are frequently used in measuring materials, dimensions, and distances.
-
Financial Calculations: Dividing assets, calculating interest, or sharing profits often involves fractional amounts.
-
Data Analysis: Many datasets involve fractional data, requiring calculations similar to the one we've discussed.
-
Time Management: Scheduling tasks or allocating time for various activities might involve fractional portions of an hour or day.
Expanding on Fraction Skills: Further Exploration
Mastering fraction manipulation opens doors to more complex mathematical concepts. Here are some related areas you might explore:
-
Adding and Subtracting Fractions: Learn to find common denominators and perform these fundamental operations.
-
Multiplying and Dividing Fractions: Explore how to simplify calculations involving multiplication and division of fractions.
-
Working with Decimals: Understanding the relationship between fractions and decimals is crucial for versatile problem-solving.
-
Solving Equations Involving Fractions: Practice incorporating fractions into algebraic equations.
-
Understanding Percentages: Percentages are essentially fractions expressed as parts of 100. Mastering fractions will help you work effectively with percentages.
Conclusion: Half of 1 and 1/4 and Beyond
This article has provided a comprehensive guide to calculating half of 1 and 1/4, highlighting different methods and emphasizing the importance of understanding fractions. We've demonstrated how this seemingly basic calculation has broad applications in diverse fields, underscoring the significance of fundamental mathematical skills. By solidifying your understanding of fractions, you equip yourself with a crucial tool for navigating a wide range of mathematical and real-world problems. Remember to practice regularly, explore related concepts, and continue learning to enhance your mathematical proficiency. The ability to confidently handle fractions opens up a world of opportunities for further mathematical exploration and problem-solving.
Latest Posts
Latest Posts
-
The Electron Transport Chain Receives High Energy Electrons From
May 09, 2025
-
Half Of 1 And A Half
May 09, 2025
-
Find The Next Three Terms In The Sequence
May 09, 2025
-
How To Do Splitting The Middle Term
May 09, 2025
-
Chemical Reactions That Absorb Energy Are Said To Be
May 09, 2025
Related Post
Thank you for visiting our website which covers about What's Half Of 1 And 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.