Half Of 1 And A Half
listenit
May 09, 2025 · 4 min read
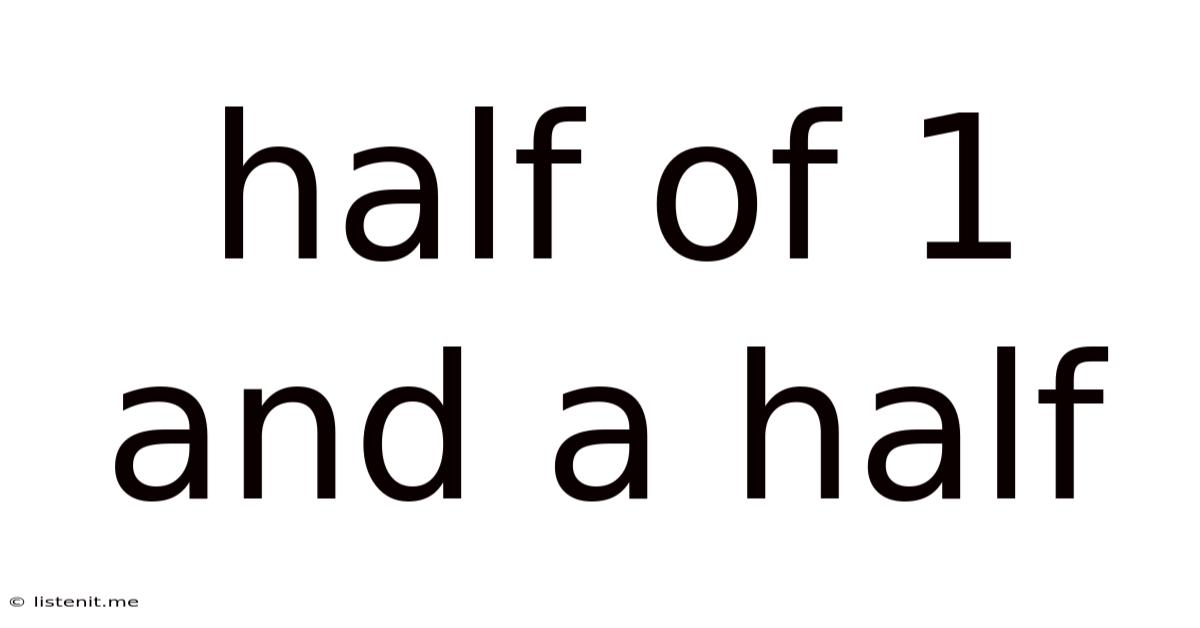
Table of Contents
Half of One and a Half: Unpacking the Math and its Implications
The seemingly simple question, "What is half of one and a half?", often trips people up. While the answer might seem obvious at first glance, a deeper dive reveals interesting mathematical concepts and practical applications. This article will explore this seemingly simple problem, delving into its solution, its connection to fractions and decimals, and its relevance in various real-world scenarios.
Understanding the Problem: Half of 1 ½
The phrase "half of one and a half" translates directly into a mathematical expression: ½ * 1 ½. To solve this, we need to understand how to work with fractions and mixed numbers. The core challenge lies in understanding how to multiply a fraction by a mixed number.
Converting to Improper Fractions
The most straightforward approach involves converting the mixed number (1 ½) into an improper fraction. A mixed number consists of a whole number and a fraction. To convert it, we multiply the whole number by the denominator of the fraction and add the numerator. The result becomes the new numerator, while the denominator remains the same.
Therefore, 1 ½ becomes:
(1 * 2) + 1 = 3
This gives us the improper fraction ³⁄₂.
Now our equation becomes: ½ * ³⁄₂
Multiplying Fractions
Multiplying fractions is relatively simple: multiply the numerators together and the denominators together.
(1 * 3) / (2 * 2) = ³⁄₄
Therefore, half of one and a half is ¾ or 0.75.
Different Approaches to Solving the Problem
While the improper fraction method is efficient, there are alternative ways to solve this problem. Let's explore a couple of other approaches:
Decimal Conversion Method
We can convert both numbers into decimals before performing the calculation. One and a half is equivalent to 1.5. Half is equivalent to 0.5. Therefore, the calculation becomes:
0.5 * 1.5 = 0.75
This method yields the same result as the fraction method, reinforcing the accuracy of our answer.
Division Method
Instead of multiplication, we can approach the problem using division. Finding half of a number is equivalent to dividing that number by two. So, we can divide 1 ½ by 2:
1 ½ ÷ 2
This can be solved by first converting 1 ½ to an improper fraction (³⁄₂) and then dividing by ²⁄₁ (which is equivalent to 2):
³⁄₂ ÷ ²⁄₁ = ³⁄₂ * ₁⁄₂ = ³⁄₄
Again, we arrive at the same answer: ¾ or 0.75.
Real-World Applications: Where Does This Matter?
The seemingly simple calculation of "half of one and a half" has practical applications in numerous real-world situations. Consider these examples:
Cooking and Baking:
Recipes often require precise measurements. If a recipe calls for 1 ½ cups of flour and you want to halve the recipe, knowing that half of 1 ½ cups is ¾ cups is crucial for achieving the desired result. Incorrect measurements could significantly impact the final product.
Construction and Measurement:
In construction and other trades, accurate measurements are paramount. If a project requires a piece of wood 1 ½ meters long and you need to cut it in half, understanding the calculation ensures you cut the wood to the correct length (¾ meters). Incorrect cuts can lead to waste and potentially compromise the structure.
Finance and Budgeting:
Understanding fractions and decimals is important for managing personal finances. If you have $1.50 and want to spend half, you need to know that you'll be spending $0.75. This knowledge is essential for budgeting and avoiding overspending.
Data Analysis and Statistics:
In data analysis and statistics, understanding fractions and decimals is crucial for interpreting data and making calculations. For example, if a survey shows that 1 ½ of respondents prefer a particular product, calculating half of that number would help to understand the proportion of respondents with that preference.
Expanding the Concept: Beyond One and a Half
The principle of finding half of a number extends beyond one and a half. Let's consider how this concept applies to other numbers and explore its wider implications in mathematics.
Finding Half of Other Mixed Numbers
The same methods used to find half of one and a half can be applied to find half of any mixed number. For instance, let's find half of 2 ½:
- Convert 2 ½ to an improper fraction: (2 * 2) + 1 = 5, resulting in ⁵⁄₂.
- Multiply by ½: ⁵⁄₂ * ½ = ⁵⁄₄
- Simplify (if possible): ⁵⁄₄ can be expressed as 1 ¼ or 1.25.
This demonstrates that the process remains consistent for various mixed numbers.
Generalizing the Concept: Halving Any Number
The concept of finding half a number is fundamental to the broader understanding of division and fractions. It's a core concept in mathematics that underpins more complex operations and problems. Understanding how to halve any number, whether it's a whole number, a fraction, or a decimal, is essential for various mathematical applications.
Conclusion: Mastering the Fundamentals
While seemingly simple, the question "What is half of one and a half?" highlights the importance of understanding fundamental mathematical concepts. The ability to work comfortably with fractions and decimals is crucial not just for academic success but also for navigating real-world situations. From baking a cake to managing finances, understanding these concepts equips us with the tools to solve problems accurately and efficiently. By mastering these fundamental mathematical skills, we improve our problem-solving abilities and enhance our understanding of the world around us. This seemingly simple problem serves as a reminder of the power of foundational mathematical knowledge and its far-reaching implications in our daily lives.
Latest Posts
Latest Posts
-
Is Tap Water A Pure Substance
May 11, 2025
-
Product To Sum And Sum To Product Formulas
May 11, 2025
-
Cell Division Is Necessary For An Organism To
May 11, 2025
-
What Is The Gcf Of 21 And 18
May 11, 2025
-
What Is The Uncertainty Of The Position Of The Bacterium
May 11, 2025
Related Post
Thank you for visiting our website which covers about Half Of 1 And A Half . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.