What Is The Gcf Of 21 And 18
listenit
May 11, 2025 · 5 min read
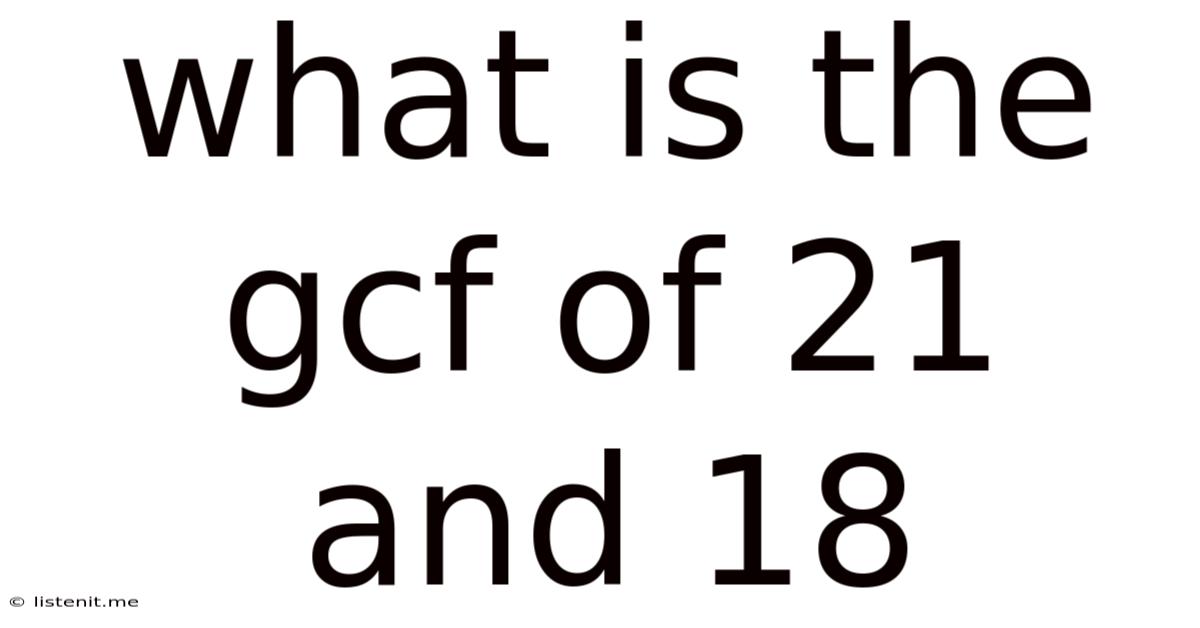
Table of Contents
What is the GCF of 21 and 18? A Deep Dive into Greatest Common Factor
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it opens up a world of mathematical possibilities. This comprehensive guide will explore the GCF of 21 and 18, providing not only the answer but also a thorough explanation of the process and its significance in mathematics and beyond.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. It's a fundamental concept in number theory with applications in various fields, including cryptography, computer science, and even music theory.
Why is finding the GCF important?
The GCF plays a crucial role in simplifying fractions, solving algebraic equations, and understanding the relationships between numbers. It helps us understand the common factors shared by two or more numbers, providing a foundation for more advanced mathematical concepts.
Methods for Finding the GCF of 21 and 18
Several methods can be used to determine the GCF of 21 and 18. We will explore three common approaches:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor.
Factors of 21: 1, 3, 7, 21
Factors of 18: 1, 2, 3, 6, 9, 18
By comparing the lists, we can see that the common factors are 1 and 3. The greatest of these common factors is 3. Therefore, the GCF of 21 and 18 is 3.
2. Prime Factorization Method
This method utilizes the prime factorization of each number to find the GCF. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
Prime factorization of 21: 3 x 7
Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
To find the GCF, we identify the common prime factors and multiply them together. Both 21 and 18 share one factor of 3. Therefore, the GCF of 21 and 18 is 3.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which represents the GCF.
Let's apply the Euclidean algorithm to 21 and 18:
- Start with the larger number (21) and the smaller number (18).
- Subtract the smaller number from the larger number: 21 - 18 = 3
- Replace the larger number with the result (3) and keep the smaller number (18).
- Repeat the subtraction: 18 - 3 - 3 - 3 - 3 - 3 - 3 = 0 (Six times)
- **The GCF is the last non-zero remainder, which is 3.
Applications of GCF in Real-World Scenarios
The seemingly simple concept of the GCF has far-reaching applications in various fields:
1. Simplifying Fractions
Finding the GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 21/18 can be simplified by dividing both the numerator and denominator by their GCF (3), resulting in the simplified fraction 7/6.
2. Geometry and Measurement
GCF is used in solving problems related to area and perimeter. For instance, if you have a rectangular garden with dimensions 21 feet by 18 feet, finding the GCF helps determine the size of the largest square tiles that can be used to cover the garden without any cutting.
3. Music Theory
Interestingly, GCF plays a role in music theory, especially in understanding musical intervals and harmonies. The GCF of two musical frequencies determines the simplicity of the interval between the notes.
Expanding the Concept: GCF of More Than Two Numbers
The methods discussed above can be extended to find the GCF of more than two numbers. For instance, to find the GCF of 21, 18, and another number (let's say 15):
-
Find the prime factorization of each number:
- 21 = 3 x 7
- 18 = 2 x 3²
- 15 = 3 x 5
-
Identify the common prime factors: The only common prime factor is 3.
-
The GCF of 21, 18, and 15 is 3.
The Euclidean algorithm can also be adapted to find the GCF of more than two numbers by repeatedly applying the algorithm to pairs of numbers until a single GCF is obtained.
Conclusion: The Power of Simple Math
While calculating the GCF of 21 and 18 might seem elementary, understanding the concept and different methods for determining it unveils its significance in various mathematical contexts. The GCF is not just a theoretical concept; it’s a practical tool with numerous applications in simplifying fractions, solving geometrical problems, and even exploring the world of music. Mastering this fundamental concept builds a strong foundation for more advanced mathematical explorations. This comprehensive exploration has gone beyond simply stating that the GCF of 21 and 18 is 3, providing a deep dive into the methods and applications, ensuring a thorough understanding for any reader. The various methods described offer flexibility based on the context and the complexity of the numbers involved. From simple factor listing to the more sophisticated Euclidean algorithm, the choice of method can be tailored to the specific situation, underscoring the versatility and importance of understanding the GCF.
Latest Posts
Latest Posts
-
Why Do Electric Field Lines Never Cross
May 13, 2025
-
1 10 As A Percent And Decimal
May 13, 2025
-
Can All Minerals Be A Gemstone
May 13, 2025
-
Multicellular Heterotrophs Without A Cell Wall
May 13, 2025
-
What Are The Gcf Of 48
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 21 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.