What's Between 1 4 And 3 8
listenit
Mar 28, 2025 · 5 min read
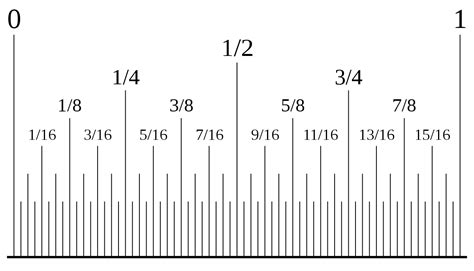
Table of Contents
What Lies Between 1/4 and 3/8? A Deep Dive into Fractions, Decimals, and More
The seemingly simple question, "What's between 1/4 and 3/8?" opens a door to a fascinating exploration of fractions, decimals, percentages, and even the infinite nature of numbers. While the immediate answer might appear straightforward, delving deeper reveals a rich tapestry of mathematical concepts and practical applications. This article will not only provide the answer but also illuminate the underlying principles and demonstrate their relevance in everyday life.
Understanding Fractions: The Building Blocks
Before diving into the specifics of the interval between 1/4 and 3/8, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we're considering.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into.
In our case, we're dealing with fractions that have a common denominator, making comparisons and calculations easier.
Finding the Common Ground: Equivalent Fractions
The first step to finding what lies between 1/4 and 3/8 is to express both fractions with a common denominator. The least common multiple (LCM) of 4 and 8 is 8. Therefore, we can rewrite 1/4 as an equivalent fraction with a denominator of 8:
1/4 = (1 x 2) / (4 x 2) = 2/8
Now we have a clearer picture: We need to find what's between 2/8 and 3/8.
The Answer: Simple and Elegant
The simplest answer is that nothing whole lies directly between 2/8 and 3/8. There's no other fraction with a denominator of 8 that falls within this range. However, this doesn't mean there are no numbers between them. The number line is continuous, meaning there are infinitely many numbers between any two distinct numbers.
Exploring the Infinite: Decimal Representation
To visualize the numbers between 2/8 and 3/8, let's convert these fractions into decimals:
- 2/8 = 0.25
- 3/8 = 0.375
Now we can see that numbers like 0.26, 0.27, 0.275, 0.3, 0.35, and countless others lie between 0.25 and 0.375. Each of these decimals represents a fraction, though many would require larger denominators to express them precisely.
Expanding the Possibilities: Finding Intermediate Fractions
We can find fractions between 2/8 and 3/8 by increasing the denominator. For example, if we double the denominator to 16, we can find fractions like:
- 5/16 (which is 0.3125)
- 6/16 (which simplifies to 3/8)
By increasing the denominator further, we can find an infinite number of fractions between 2/8 and 3/8. This demonstrates the density of rational numbers on the number line.
Beyond Fractions: Percentages and Real-World Applications
Converting our fractions to percentages provides another perspective.
- 2/8 = 25%
- 3/8 = 37.5%
This representation is particularly useful in everyday situations. For example, if you're tracking progress on a project, you might say you're 26% complete, representing a value between 25% and 37.5%. This illustrates how fractions, decimals, and percentages are interconnected and applied practically.
Delving Deeper: Irrational Numbers
While we've focused on rational numbers (numbers that can be expressed as a fraction), it's crucial to acknowledge the existence of irrational numbers between 1/4 and 3/8. Irrational numbers cannot be expressed as a simple fraction; their decimal representation goes on forever without repeating. Numbers like √2 (the square root of 2) or π (pi) are examples. Even though we can't precisely express them as fractions with finite decimals, infinitely many irrational numbers exist within our range.
Practical Applications in Various Fields
Understanding the nuances of numbers between fractions has far-reaching applications across various fields:
- Engineering and Physics: Precision is paramount. Calculations involving dimensions, forces, or speeds often require considering values between fractional measurements.
- Finance and Accounting: Calculating interest rates, determining profit margins, or analyzing investment returns often involves working with fractions and decimals.
- Computer Science: Representing data and performing calculations often involve binary representations (base-2), which are closely related to fractions.
- Statistics and Probability: Analyzing data sets and calculating probabilities involves working with fractions and percentages to represent relative frequencies.
- Measurement and Surveying: Accurate measurements necessitate understanding and utilizing fractions and decimals with precision.
The Importance of Number Sense and Mathematical Intuition
The seemingly simple question regarding what lies between 1/4 and 3/8 underscores the importance of developing strong number sense and mathematical intuition. It encourages us to move beyond rote memorization and to explore the underlying concepts that govern numbers and their relationships. Mastering these skills empowers us to tackle complex problems and enhances our analytical abilities in various aspects of life.
Conclusion: A Journey Beyond the Obvious
The exploration of the interval between 1/4 and 3/8 has taken us on a journey beyond a simple arithmetic problem. We've uncovered the interconnectedness of fractions, decimals, and percentages, explored the infinite nature of numbers, and touched upon their wide-ranging applications. This journey highlights the beauty and power of mathematics and the importance of developing a strong understanding of its fundamental principles. By understanding these concepts, we can confidently navigate the world of numbers and apply our knowledge to solve real-world problems with greater accuracy and precision. The seemingly small space between 1/4 and 3/8 contains a universe of mathematical richness, waiting to be explored. The more we delve into it, the greater our appreciation for the complexity and beauty of mathematics becomes. This continuous exploration enhances our understanding and helps build stronger analytical and problem-solving skills, essential in various aspects of life.
Latest Posts
Latest Posts
-
27 4 As A Mixed Number
Mar 31, 2025
-
Is Burning A Match A Chemical Change
Mar 31, 2025
-
What Is The Difference Between A Solution And A Suspension
Mar 31, 2025
-
What Is The Symbol Of Aluminum
Mar 31, 2025
-
42 Is 70 Of What Number
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What's Between 1 4 And 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
