What's 1 2 Of 3 4
listenit
May 12, 2025 · 5 min read
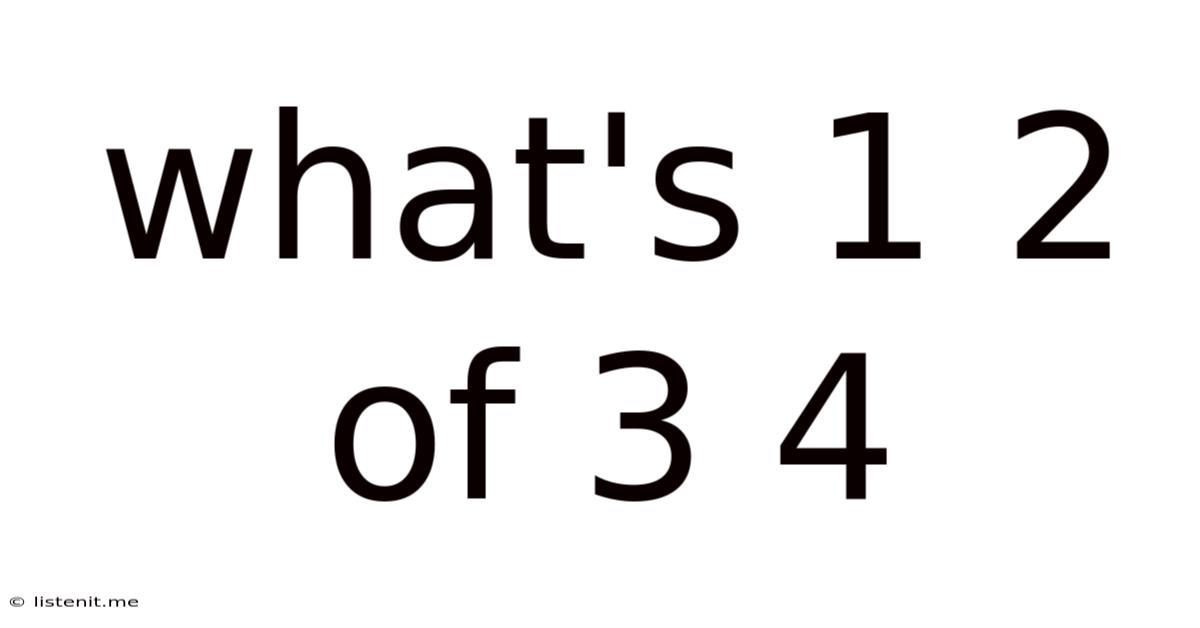
Table of Contents
What's 1 2 of 3 4? Unpacking Mathematical Ambiguity and Order of Operations
The seemingly simple question, "What's 1 2 of 3 4?" is deceptively complex. Its ambiguity lies not in advanced mathematical concepts, but in the lack of explicit operators and the inherent order of operations. This article will delve into the nuances of this problem, exploring different interpretations, highlighting the critical role of mathematical notation, and demonstrating the importance of precise communication in mathematics. We’ll uncover why this simple-looking question can lead to multiple answers and how to avoid such ambiguity in the future.
Understanding the Problem: The Absence of Explicit Operators
The core issue stems from the absence of clearly defined operators between the numbers. We have four numbers: 1, 2, 3, and 4, but no plus (+), minus (-), multiplication (×), or division (÷) symbols explicitly stated. This lack of explicit operators allows for multiple interpretations, each leading to a different result. This ambiguity is a crucial lesson in the importance of precise mathematical notation. Without clear operators, the question is ill-defined.
Possible Interpretations and Solutions
Let's explore several plausible interpretations of "1 2 of 3 4," each leading to a unique answer. We'll analyze these interpretations through the lens of order of operations (PEMDAS/BODMAS), remembering that without explicit operators, we need to infer them based on conventional mathematical practices.
Interpretation 1: Multiplication and Implicit Multiplication
One common interpretation is to assume implicit multiplication. "Of" frequently implies multiplication in mathematical contexts. We could read the expression as:
(1 × 2) × (3 × 4)
Following the order of operations (multiplication before addition or subtraction), we get:
2 × 12 = 24
Therefore, under this interpretation, the answer is 24. This interpretation prioritizes grouping based on the proximity of numbers and the implicit meaning of "of".
Interpretation 2: Multiplication with a Different Grouping
Another plausible interpretation involves a different grouping of the multiplication:
1 × (2 × 3) × 4
Following the order of operations (performing multiplications from left to right), we have:
1 × 6 × 4 = 24
Interestingly, this interpretation also yields 24. This demonstrates that certain groupings, even with implicit multiplication, can still lead to the same result.
Interpretation 3: Fraction Interpretation:
A less conventional, but still mathematically valid, interpretation involves treating "of" as a fractional representation:
(1/2) * (3/4)
This treats "1 2" as the fraction 1/2 and "3 4" as the fraction 3/4. Multiplying these fractions gives us:
(1/2) × (3/4) = 3/8
Thus, under this interpretation, the answer is 3/8 or 0.375. This highlights the crucial role of context and the need for precise mathematical notation to avoid such ambiguity.
Interpretation 4: Mixed Number Interpretation:
Another possible interpretation involves reading "1 2" and "3 4" as mixed numbers:
1 2/1 and 3 4/1
However, this interpretation introduces fractions without a clear multiplication or division operation between them, leaving the expression still indeterminate.
Interpretation 5: Concatenation
Although less likely in a mathematical context, one could interpret the expression as a concatenation of digits, resulting in the number 1234. While not a standard mathematical interpretation, it's important to acknowledge this possibility to demonstrate the range of interpretations that can arise from ambiguous notation.
The Crucial Role of Mathematical Notation
The ambiguity inherent in "What's 1 2 of 3 4?" underscores the critical importance of precise mathematical notation. The lack of explicit operators leaves the expression open to multiple valid interpretations. In mathematics, precision is paramount. Ambiguous expressions can lead to errors, confusion, and ultimately, incorrect results.
Avoiding Ambiguity: Best Practices
To avoid similar ambiguities in the future, adhere to these best practices:
-
Use Explicit Operators: Always use explicit operators (+, -, ×, ÷) to clearly indicate the intended mathematical operations.
-
Use Parentheses for Grouping: Parentheses ( ) or brackets [ ] are crucial for specifying the order of operations and avoiding any confusion about the intended grouping of numbers.
-
Context is Key: The context in which the expression appears can sometimes provide clues about the intended interpretation. However, relying solely on context is risky and should be avoided whenever possible.
-
Define Variables: If you are working with variables or unknown quantities, always clearly define them before using them in an expression.
-
Verify and Clarify: If you encounter an ambiguous mathematical expression, seek clarification from the source to ensure you understand the intended meaning before attempting to solve it.
Expanding the Discussion: Implications in Programming and Computer Science
The issues raised by the ambiguity of "1 2 of 3 4" have significant implications in programming and computer science. Programming languages, unlike human language, require precise syntax and unambiguous instructions. If a programming expression is unclear, the compiler or interpreter will generate an error. This emphasizes the rigorousness required in programming to avoid errors stemming from unclear instructions.
Different programming languages handle operator precedence differently, potentially yielding different results for a poorly defined expression. Therefore, using explicit operators and parentheses is even more critical in programming to avoid unexpected behavior and errors.
Conclusion: Precision and Clarity in Mathematics
The seemingly simple question, "What's 1 2 of 3 4?", serves as a powerful illustration of the need for precision and clarity in mathematical notation. The multiple possible interpretations and solutions highlight the importance of using explicit operators, parentheses, and clear definitions to prevent ambiguity. This lesson applies not only to mathematical computations but also to the broader fields of programming, engineering, and any discipline requiring precise communication of quantitative information. By adhering to best practices in mathematical notation, we can avoid confusion, errors, and ensure accurate and consistent results. The seemingly trivial question becomes a valuable reminder of the foundational principles of mathematical accuracy and the potential consequences of ambiguous notation. Always strive for clarity and leave no room for misinterpretation in your mathematical expressions.
Latest Posts
Latest Posts
-
Which Of The Following Is A Scalar
May 12, 2025
-
80 Of What Number Is 160
May 12, 2025
-
A Chlorine Isotope With 20 Neutrons
May 12, 2025
-
A Possible Explanation For An Observation
May 12, 2025
-
What Is 4 1 3 As A Fraction
May 12, 2025
Related Post
Thank you for visiting our website which covers about What's 1 2 Of 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.