What Is 4 1 3 As A Fraction
listenit
May 12, 2025 · 5 min read
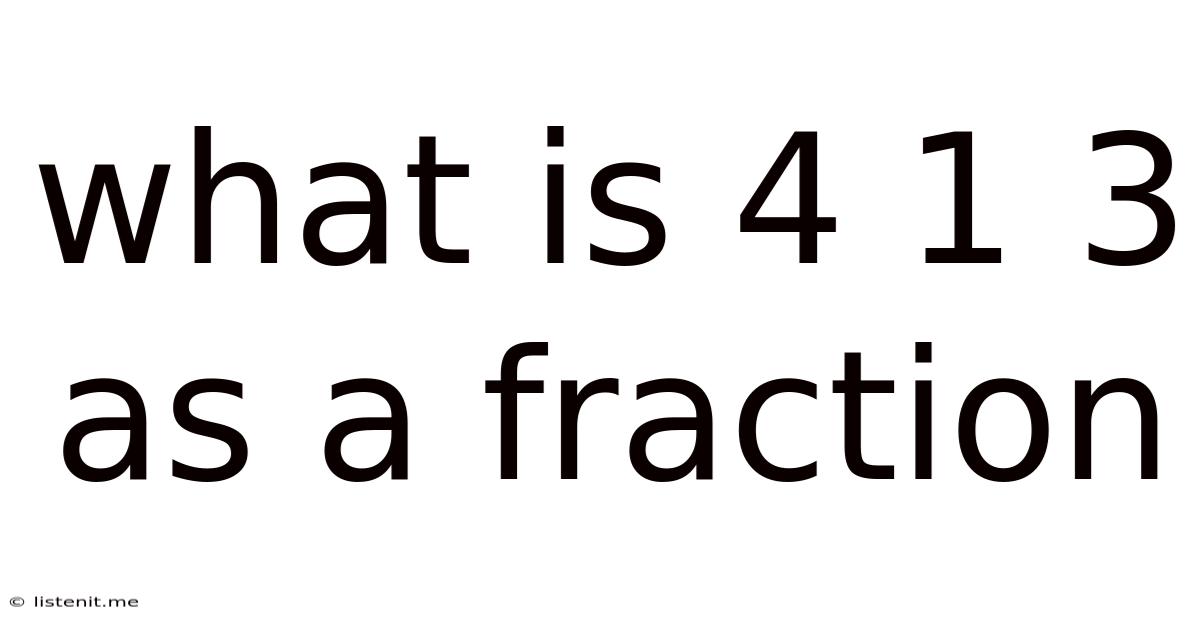
Table of Contents
What is 4 1/3 as a Fraction? A Comprehensive Guide
Understanding fractions is a fundamental concept in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve into the process of converting the mixed number 4 1/3 into an improper fraction, explaining the underlying principles and providing practical examples to solidify your understanding. We'll also explore related concepts and offer tips for mastering fraction conversions.
Understanding Mixed Numbers and Improper Fractions
Before we dive into the conversion, let's clarify the terminology.
Mixed numbers combine a whole number and a fraction, like 4 1/3. They represent a quantity greater than one.
Improper fractions, on the other hand, have a numerator (top number) that is greater than or equal to the denominator (bottom number). For example, 13/3 is an improper fraction.
Converting a mixed number to an improper fraction is a common task, and understanding this process is key to performing various mathematical operations.
Converting 4 1/3 to an Improper Fraction: A Step-by-Step Guide
The conversion of 4 1/3 to an improper fraction involves a simple, two-step process:
Step 1: Multiply the whole number by the denominator.
In our example, the whole number is 4, and the denominator of the fraction is 3. Multiplying these together gives us: 4 * 3 = 12
Step 2: Add the numerator to the result from Step 1.
The numerator of our fraction is 1. Adding this to the result from Step 1 (12), we get: 12 + 1 = 13
Step 3: Keep the denominator the same.
The denominator of the original fraction remains unchanged. Therefore, the denominator of our improper fraction will be 3.
Step 4: Combine the results to form the improper fraction.
Combining the results from Step 2 (13) and Step 3 (3), we arrive at our final improper fraction: 13/3
Therefore, 4 1/3 is equal to 13/3.
Visualizing the Conversion
It can be helpful to visualize this conversion. Imagine you have four whole pies, each divided into three equal slices. The 4 1/3 represents four whole pies and one additional slice from a fifth pie, where each pie has three slices. If you count all the slices, you have 13 slices in total. Since each pie was divided into 3 slices, you have 13/3 slices. This visual representation reinforces the mathematical process.
Practical Applications of Improper Fractions
Improper fractions are incredibly useful in various mathematical contexts:
-
Addition and Subtraction of Fractions: It's often easier to add and subtract fractions when they are in improper fraction form. Having a common denominator is crucial for these operations, and converting to improper fractions simplifies this process.
-
Multiplication and Division of Fractions: While you can multiply and divide mixed numbers, it’s often more efficient to convert them to improper fractions first, simplifying the calculations.
-
Solving Equations: Many algebraic equations involve fractions. Converting mixed numbers to improper fractions helps in solving these equations more effectively.
-
Real-World Problems: Numerous real-world scenarios require working with fractions. Consider situations involving measuring ingredients in cooking, calculating distances, or dividing resources. Converting between mixed numbers and improper fractions ensures accurate calculations in these contexts.
Further Exploring Fraction Conversions
Mastering fraction conversions is crucial for building a strong foundation in mathematics. Here are some related concepts to explore:
-
Converting Improper Fractions to Mixed Numbers: The reverse process – converting an improper fraction back to a mixed number – involves division. Divide the numerator by the denominator. The quotient becomes the whole number, the remainder becomes the numerator, and the denominator stays the same.
-
Simplifying Fractions: After converting to an improper fraction or performing calculations, it's often necessary to simplify the fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD.
-
Comparing Fractions: Knowing how to convert between different fraction forms is crucial when comparing the relative sizes of fractions. Converting to improper fractions can make it easier to compare fractions with different denominators.
Tips for Mastering Fraction Conversions
-
Practice Regularly: The key to mastering any mathematical concept is consistent practice. Work through various examples, starting with simple conversions and gradually increasing the complexity.
-
Use Visual Aids: Visual aids, such as diagrams or real-world objects, can greatly enhance your understanding and make the conversion process more intuitive.
-
Break Down the Steps: Don’t try to rush the process. Take your time, break down the steps systematically, and double-check your work at each stage.
-
Seek Help When Needed: Don't hesitate to seek help from teachers, tutors, or online resources if you encounter difficulties. Many online resources offer interactive exercises and tutorials that can help you solidify your understanding.
Conclusion
Converting a mixed number like 4 1/3 to its equivalent improper fraction, 13/3, is a fundamental skill in mathematics. This seemingly simple conversion forms the basis for many more complex calculations and problem-solving exercises. By understanding the process, visualizing the concept, and practicing regularly, you can build a strong foundation in fractions and confidently tackle various mathematical challenges that involve mixed numbers and improper fractions. Remember to apply these concepts to real-world scenarios to enhance your comprehension and retention of this crucial mathematical skill. Consistent practice and a clear understanding of the underlying principles will empower you to master fraction conversions and excel in your mathematical endeavors.
Latest Posts
Latest Posts
-
Matter Is Anything That Has And Takes Up
May 12, 2025
-
When Do Parentheses Appear In The Formulas Of Ionic Compounds
May 12, 2025
-
What Percentage Of 20 Is 1
May 12, 2025
-
What Is 28 In A Fraction
May 12, 2025
-
What Is The Current Model Of An Atom Called
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 1 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.