80 Of What Number Is 160
listenit
May 12, 2025 · 5 min read
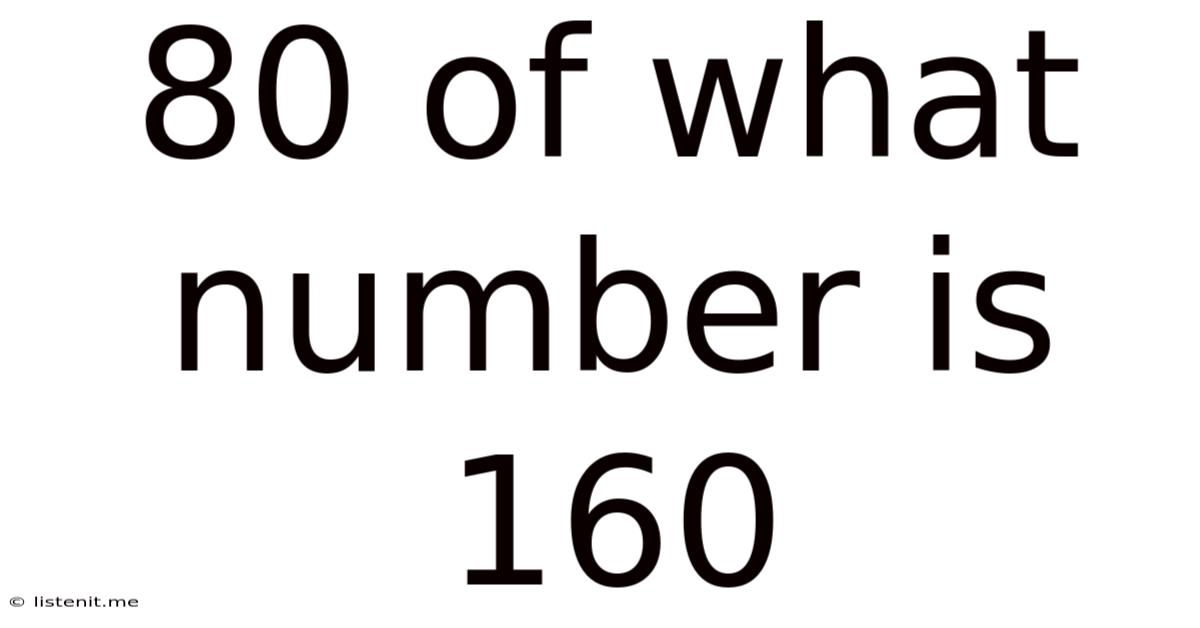
Table of Contents
80% of What Number is 160? Understanding Percentages and Problem-Solving
This seemingly simple question, "80% of what number is 160?", opens the door to understanding a fundamental concept in mathematics: percentages. While the answer might seem immediately apparent to some, exploring the various methods of solving this problem and the broader implications of percentage calculations is crucial for building a strong mathematical foundation. This article will delve into different approaches to solving this specific problem and provide a comprehensive overview of percentage calculations, equipping you with the skills to tackle similar problems with confidence.
Understanding Percentages
Before we dive into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5.
Understanding this fundamental concept is key to solving percentage problems. We can represent percentages in three main forms:
- Fraction: Expressing the percentage as a fraction with a denominator of 100 (e.g., 80% = 80/100).
- Decimal: Converting the percentage to a decimal by dividing by 100 (e.g., 80% = 0.80).
- Percentage: The standard percentage notation (e.g., 80%).
The ability to easily convert between these forms is essential for efficient problem-solving.
Method 1: Using the Equation
The most direct way to solve "80% of what number is 160?" is to set up an algebraic equation. Let's represent the unknown number as 'x'. We can translate the problem into an equation:
0.80x = 160
To solve for 'x', we need to isolate it. We can do this by dividing both sides of the equation by 0.80:
x = 160 / 0.80
x = 200
Therefore, 80% of 200 is 160.
This method is straightforward and efficient, particularly for those comfortable with algebraic manipulation.
Method 2: Using Proportions
Another effective approach is using proportions. We can set up a proportion relating the percentage to the corresponding parts:
80/100 = 160/x
This proportion states that the ratio of 80 to 100 is equal to the ratio of 160 to the unknown number 'x'. To solve for 'x', we can cross-multiply:
80x = 160 * 100
80x = 16000
Now, divide both sides by 80:
x = 16000 / 80
x = 200
Again, we arrive at the solution: 80% of 200 is 160. This method provides a visual representation of the relationship between the percentage and the quantities involved.
Method 3: Working Backwards from the Percentage
We can also approach this problem by considering what 1% represents. If 80% of a number is 160, then we can find the value of 1% by dividing 160 by 80:
160 / 80 = 2
This means 1% of the number is 2. Since there are 100% in a whole, we can find the total number by multiplying 2 by 100:
2 * 100 = 200
Therefore, the number is 200. This method is intuitive and helps visualize the proportional relationships.
Real-World Applications of Percentage Calculations
Understanding percentage calculations extends far beyond simple mathematical problems. These skills are invaluable in various real-world scenarios, including:
- Finance: Calculating interest rates, discounts, taxes, profits, and losses. For example, understanding how much you'll pay after a 20% discount on a purchase.
- Statistics: Analyzing data sets, interpreting survey results, and understanding statistical significance. Think of election results or market research data.
- Science: Determining percentages of components in mixtures, calculating experimental yields, and interpreting scientific data.
- Everyday Life: Calculating tips in restaurants, understanding sale prices, comparing different products based on their prices and features.
Advanced Percentage Problems and Solving Strategies
While the problem "80% of what number is 160?" is relatively straightforward, more complex percentage problems can arise. Here are some advanced scenarios and strategies to tackle them:
-
Successive Percentages: These involve applying multiple percentages sequentially. For example, finding the final price after a 10% discount followed by a 5% sales tax. It's crucial to remember that these percentages don't simply add up; they are applied successively.
-
Percentage Increase/Decrease: These problems involve finding the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] x 100%.
-
Percentage of a Percentage: This involves finding a percentage of a percentage itself. For example, "Find 25% of 40% of 500". This requires performing the percentage calculations step by step.
-
Solving for Unknown Percentages: Some problems involve finding the percentage when the original number and the resulting amount are known. This often requires setting up an equation and solving for the unknown percentage.
To effectively solve these advanced problems, a strong grasp of fundamental percentage principles, algebraic manipulation, and careful attention to detail is essential.
Practical Tips for Mastering Percentage Calculations
-
Practice Regularly: Consistent practice is key to mastering any mathematical concept. Solve various percentage problems to build your confidence and proficiency.
-
Visual Aids: Use diagrams, charts, or other visual aids to represent the problem and make it easier to understand.
-
Check your Work: Always double-check your calculations to ensure accuracy. Using a calculator can help minimize calculation errors.
-
Break Down Complex Problems: Divide complex problems into smaller, more manageable parts. This simplifies the process and makes it easier to identify and solve each step.
-
Understand the Context: Pay close attention to the wording of the problem to understand exactly what is being asked.
Conclusion
The question "80% of what number is 160?" serves as an excellent introduction to the world of percentage calculations. By understanding the various methods of solving this problem—using equations, proportions, or working backwards—we can develop a strong foundation for tackling more complex percentage problems. The applications of percentage calculations are vast and permeate various aspects of our lives, making it a crucial skill to master. Through consistent practice and a solid understanding of the underlying principles, you can confidently navigate the world of percentages and apply these skills to solve real-world problems with ease. Remember to always check your work and break down complex problems into smaller, more manageable steps. With dedication and practice, mastery of percentage calculations is well within your reach.
Latest Posts
Latest Posts
-
Anything With Weight And That Takes Up Space
May 12, 2025
-
Gases At Room Temperature On The Periodic Table
May 12, 2025
-
0 82 As A Fraction In Simplest Form
May 12, 2025
-
The Balanced Combustion Reaction For C6h6 Is
May 12, 2025
-
How To Know The Number Of Neutrons
May 12, 2025
Related Post
Thank you for visiting our website which covers about 80 Of What Number Is 160 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.