What Percentage Of 100 Is 15
listenit
May 25, 2025 · 4 min read
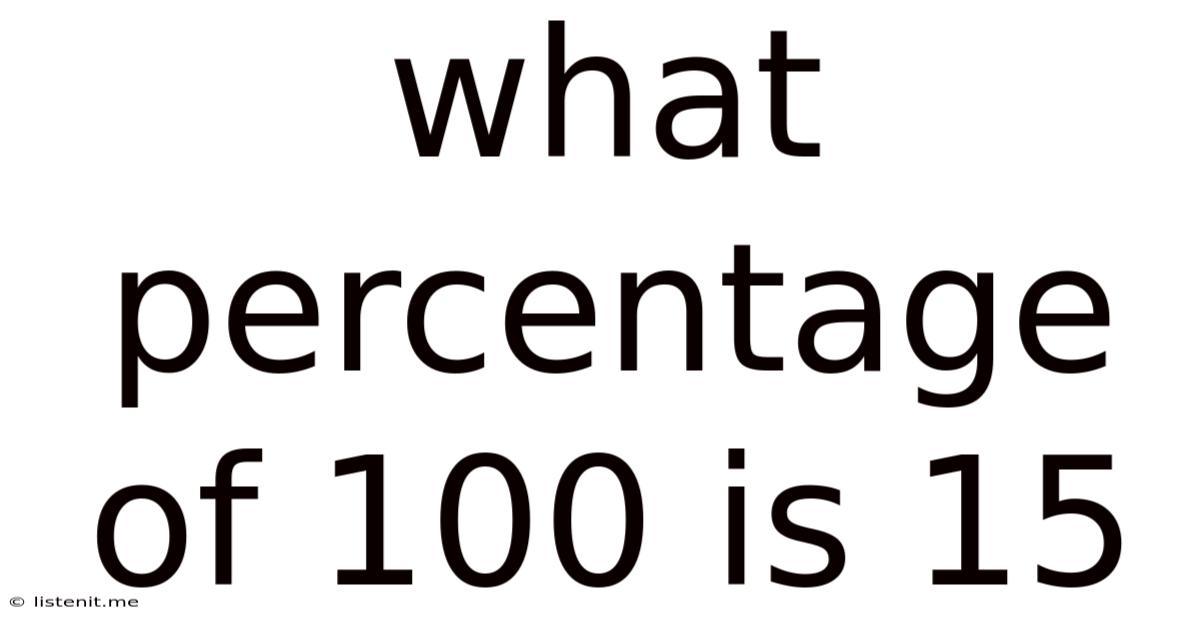
Table of Contents
What Percentage of 100 is 15? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and taxes to comprehending statistical data and financial reports. This article will delve into the question, "What percentage of 100 is 15?" and, more importantly, will equip you with the knowledge and techniques to solve any percentage problem with ease. We'll explore different methods, provide practical examples, and touch upon the broader implications of percentage calculations.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of 100." Therefore, 15% means 15 out of 100, or 15/100. This fundamental understanding is the cornerstone of all percentage calculations.
Method 1: The Direct Approach
The most straightforward way to determine what percentage of 100 is 15 is to use a simple proportion:
15/100 = x/100
Where 'x' represents the percentage we want to find. In this case, the equation is already set up for us. The answer is directly apparent: 15/100 = 15%. Therefore, 15 is 15% of 100.
Method 2: Using Decimal Conversion
We can also solve this using decimal conversions. A percentage can be easily converted to a decimal by dividing it by 100. Conversely, a decimal can be converted to a percentage by multiplying it by 100.
In this case, we want to find what percentage 15 represents of 100. First, we express the fraction as a decimal:
15/100 = 0.15
To convert this decimal to a percentage, we multiply by 100:
0.15 * 100 = 15%
This confirms our previous finding: 15 is 15% of 100.
Method 3: The Formula Approach
A more general formula for percentage calculations is:
(Part / Whole) * 100 = Percentage
In our problem:
- Part = 15
- Whole = 100
Substituting these values into the formula:
(15 / 100) * 100 = 15%
This formula works for any percentage problem, regardless of the numbers involved.
Beyond the Basics: Solving More Complex Percentage Problems
While the problem "What percentage of 100 is 15?" is relatively simple, understanding the underlying principles allows you to tackle more complex percentage calculations. Let's explore some examples:
Example 1: Finding the Percentage of a Different Whole Number
What percentage of 250 is 75?
Using the formula:
(75 / 250) * 100 = 30%
Therefore, 75 is 30% of 250.
Example 2: Finding the Whole Number Given a Percentage and Part
If 20% of a number is 40, what is the number?
Let's represent the unknown number as 'x'. We can set up the equation:
(20/100) * x = 40
Solving for x:
x = (40 * 100) / 20 = 200
Therefore, the number is 200.
Example 3: Calculating Percentage Increase or Decrease
A product's price increased from $50 to $60. What is the percentage increase?
First, calculate the difference: $60 - $50 = $10
Then, divide the difference by the original price and multiply by 100:
($10 / $50) * 100 = 20%
The price increased by 20%.
Practical Applications of Percentage Calculations
Understanding percentages is crucial in various real-world scenarios:
- Finance: Calculating interest rates, discounts, taxes, and investment returns.
- Retail: Determining sale prices, profit margins, and markups.
- Statistics: Interpreting data, analyzing trends, and drawing conclusions from surveys and polls.
- Science: Expressing experimental results, calculating error margins, and representing proportions.
- Everyday Life: Understanding tips, calculating savings, and comparing prices.
Mastering Percentages: Tips and Tricks
- Practice regularly: The more you practice, the more comfortable you'll become with percentage calculations.
- Use a calculator: For more complex calculations, a calculator can be a valuable tool.
- Understand the concepts: Don't just memorize formulas; understand the underlying principles.
- Break down complex problems: Divide larger problems into smaller, more manageable steps.
- Check your work: Always double-check your calculations to ensure accuracy.
Conclusion: The Power of Percentages
This article has demonstrated that determining "what percentage of 100 is 15" is not just a simple arithmetic problem but a gateway to understanding a fundamental mathematical concept with broad applications. By mastering percentage calculations, you equip yourself with a powerful tool for navigating various aspects of life, from managing finances to interpreting data and making informed decisions. The methods and examples provided offer a solid foundation for further exploration and application of this vital skill. Remember to practice regularly, and you'll soon find yourself confidently tackling even the most complex percentage problems.
Latest Posts
Latest Posts
-
Whats The Date 6 Months From Now
May 25, 2025
-
7 Divided By 9 As A Fraction
May 25, 2025
-
How Many Days Is 17000 Minutes
May 25, 2025
-
How Many Hours In Three Months
May 25, 2025
-
What Is 100 To The Power Of 6
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 100 Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.