What Is 100 To The Power Of 6
listenit
May 25, 2025 · 5 min read
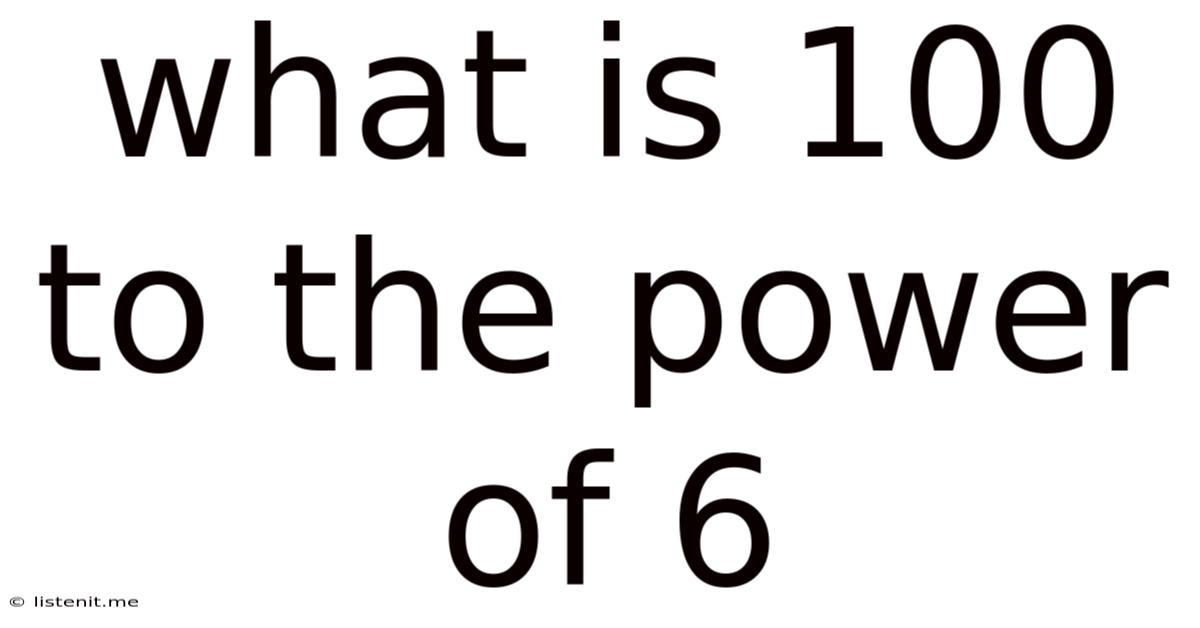
Table of Contents
What is 100 to the Power of 6? Unpacking Exponents and Their Applications
Have you ever wondered what happens when you raise a number to a significant power? Let's delve into the fascinating world of exponents, specifically addressing the question: What is 100 to the power of 6? This seemingly simple calculation opens a door to understanding fundamental mathematical concepts and their wide-ranging applications in various fields.
Understanding Exponents
Before we tackle the main question, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. For instance, in the expression 10<sup>2</sup>, 10 is the base, and 2 is the exponent. This means 10 is multiplied by itself twice: 10 x 10 = 100.
Key Terminology:
- Base: The number being multiplied.
- Exponent: The number indicating how many times the base is multiplied by itself.
- Power: Another term for exponent.
Calculating 100 to the Power of 6
Now, let's address the core question: What is 100<sup>6</sup>? This means multiplying 100 by itself six times:
100 x 100 x 100 x 100 x 100 x 100
Manually calculating this can be tedious. However, we can simplify the process using the properties of exponents and the power of 10. Since 100 is 10<sup>2</sup>, we can rewrite the expression as:
(10<sup>2</sup>)<sup>6</sup>
Using the rule of exponents, (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup>, we can simplify further:
10<sup>(2 x 6)</sup> = 10<sup>12</sup>
This means 100 to the power of 6 is equal to 10 to the power of 12. This is a much easier calculation to visualize. 10<sup>12</sup> is one trillion.
Therefore, 100<sup>6</sup> = 1,000,000,000,000
Applications of Exponents and Large Numbers
The concept of exponents, particularly with large numbers like 10<sup>12</sup>, has profound implications across numerous fields. Let's explore some examples:
1. Science and Engineering:
- Astronomy: Distances in space are often measured in astronomical units or light-years, which involve extremely large numbers expressed using exponents. Understanding exponents is crucial for comprehending the vast scales of the universe.
- Physics: Many physics equations involve exponents, for example, in describing the relationship between force, mass, and acceleration (Newton's second law).
- Chemistry: Avogadro's number (approximately 6.022 x 10<sup>23</sup>), representing the number of atoms or molecules in one mole of a substance, showcases the significance of exponents in understanding chemical quantities.
- Computer Science: Data storage capacity is often measured in bytes, kilobytes, megabytes, gigabytes, terabytes, and beyond, all using powers of 10 or 2.
2. Finance and Economics:
- Compound Interest: The power of compound interest, where interest is earned on both the principal and accumulated interest, is governed by exponential growth. Understanding exponential growth is critical for making sound financial decisions.
- Economic Modeling: Economic models frequently employ exponential functions to represent growth rates, population dynamics, and other key economic variables.
3. Biology:
- Population Growth: Exponential functions are often used to model population growth, both for humans and other organisms. Understanding the rate of exponential growth allows scientists to predict future population sizes.
4. Everyday Life:
- Data Sizes: When dealing with large files on your computer or phone, you'll encounter terms like gigabytes (GB) and terabytes (TB), which are based on powers of 10 or 2. Understanding these units helps you manage your digital storage effectively.
Working with Large Numbers and Scientific Notation
When dealing with extremely large numbers like one trillion (10<sup>12</sup>), scientific notation becomes an indispensable tool. Scientific notation expresses numbers in the form a x 10<sup>b</sup>, where 'a' is a number between 1 and 10, and 'b' is an integer representing the power of 10.
For example, 1,000,000,000,000 in scientific notation is 1 x 10<sup>12</sup>. This notation simplifies the representation of very large or very small numbers, making them easier to work with in calculations and comparisons.
Beyond the Calculation: Exploring Mathematical Concepts
The seemingly simple calculation of 100<sup>6</sup> provides a springboard to explore various mathematical concepts:
1. Order of Operations (PEMDAS/BODMAS):
Understanding the order of operations is crucial when dealing with more complex expressions involving exponents. Remember the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). This order ensures consistent and accurate results.
2. Properties of Exponents:
Several properties govern how exponents behave in calculations. Mastering these properties, such as the product rule (a<sup>m</sup> x a<sup>n</sup> = a<sup>m+n</sup>), the quotient rule (a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>), and the power rule ((a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup>), allows for efficient manipulation of exponential expressions.
3. Logarithms:
Logarithms are the inverse of exponents. They provide a way to solve for the exponent when the base and the result are known. For example, if 10<sup>x</sup> = 1000, the logarithm base 10 of 1000 (log<sub>10</sub>1000) is 3.
Conclusion: The Significance of 100 to the Power of 6
The answer to "What is 100 to the power of 6?" is more than just a numerical result. It's a gateway to understanding the power and applications of exponents in various fields. From the vastness of space to the intricacies of financial markets, the concept of exponents provides a framework for comprehending and manipulating large numbers, contributing to advancements in science, technology, and our everyday lives. The ability to simplify complex exponential expressions, utilize scientific notation, and grasp the fundamental properties of exponents is essential for anyone seeking a deeper understanding of mathematics and its real-world applications. Mastering these concepts opens up a world of possibilities and empowers you to tackle more complex mathematical challenges with confidence.
Latest Posts
Latest Posts
-
12 Divided By 5 With Remainder
May 25, 2025
-
10 Out Of 23 As A Percentage
May 25, 2025
-
What Is The Gcf Of 18 And 35
May 25, 2025
-
What Is 72 Hours From Monday At 6pm
May 25, 2025
-
How Old Are You If Your Born In 1982
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 100 To The Power Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.