12 Divided By 5 With Remainder
listenit
May 25, 2025 · 5 min read
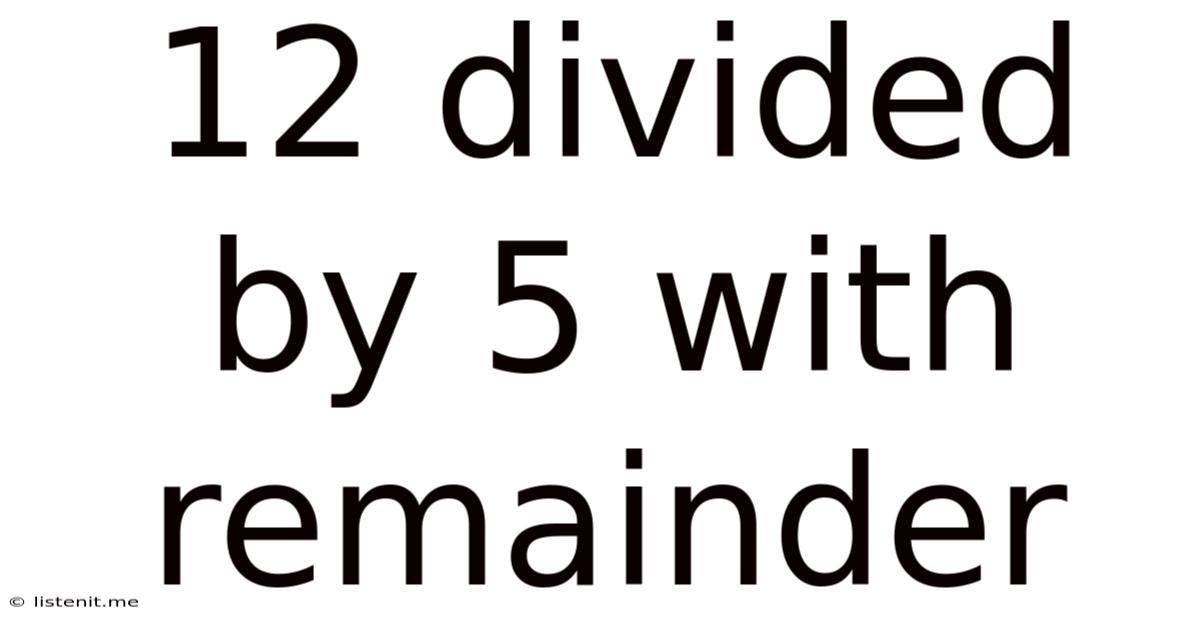
Table of Contents
12 Divided by 5 with Remainder: A Deep Dive into Division and Remainders
Understanding division, especially with remainders, is a fundamental concept in mathematics. It forms the basis for more advanced topics and has practical applications in various fields. This article will comprehensively explore the seemingly simple problem of 12 divided by 5, delving deep into the mechanics, the underlying principles, and the broader implications of division with remainders. We'll explore various methods, discuss real-world applications, and touch on related mathematical concepts.
The Basics of Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially asks the question: "How many times does one number (the divisor) go into another number (the dividend)?" The result is called the quotient. When the dividend is not perfectly divisible by the divisor, a remainder is left over.
In our example, 12 divided by 5 (written as 12 ÷ 5 or 12/5), we're asking how many times 5 goes into 12. Let's break it down:
- Dividend: 12 (the number being divided)
- Divisor: 5 (the number we're dividing by)
- Quotient: The whole number result of the division.
- Remainder: The amount left over after the division.
Calculating 12 Divided by 5
Several methods can help us find the quotient and remainder when dividing 12 by 5:
Method 1: Repeated Subtraction
We can repeatedly subtract the divisor (5) from the dividend (12) until we reach a number less than the divisor.
12 - 5 = 7 7 - 5 = 2
We subtracted 5 twice before reaching a number less than 5 (which is 2). Therefore:
- Quotient: 2
- Remainder: 2
Method 2: Long Division
Long division is a more formal method, especially useful for larger numbers.
2 R 2
5 | 12
10
--
2
We divide 12 by 5. 5 goes into 12 two times (5 x 2 = 10). Subtracting 10 from 12 leaves a remainder of 2.
Method 3: Using Multiplication and Subtraction
We can think of it this way: what is the largest multiple of 5 that is less than or equal to 12? That's 10 (5 x 2). The difference between 12 and 10 is the remainder.
12 - (5 x 2) = 12 - 10 = 2
Therefore:
- Quotient: 2
- Remainder: 2
The Importance of Remainders
Remainders aren't just leftover numbers; they provide crucial information. They tell us that the division isn't exact, indicating that the dividend isn't a multiple of the divisor. This has implications in various contexts:
Real-World Applications
- Sharing: If you have 12 cookies and want to share them equally among 5 friends, each friend gets 2 cookies (the quotient), and you have 2 cookies left over (the remainder).
- Measurement: If you have a 12-meter rope and need to cut it into 5-meter pieces, you can make 2 pieces (the quotient), and you'll have 2 meters of rope left (the remainder).
- Programming: Remainders are fundamental in computer programming, especially in tasks involving modular arithmetic and generating patterns. The modulo operator (%) gives the remainder of a division. For example,
12 % 5returns 2. - Time: Converting minutes to hours and minutes involves remainders. 127 minutes is equal to 2 hours and 7 minutes (127 / 60 = 2 with a remainder of 7).
- Scheduling: Remainders can be useful when creating schedules or rotations that need to cycle through a fixed number of slots.
- Cryptography: Modular arithmetic, which heavily relies on remainders, is a cornerstone of modern cryptography.
Beyond the Basics: Exploring Related Concepts
Understanding 12 divided by 5 with its remainder opens doors to various mathematical concepts:
Modular Arithmetic (Modulo Operation)
Modular arithmetic deals with remainders. The modulo operation (denoted by %) gives the remainder after division. In our case, 12 mod 5 = 2. This is widely used in cryptography and computer science.
Fractions and Decimals
While the above methods give us the whole number quotient and remainder, we can also express the division as a fraction (12/5) or a decimal (2.4). The fraction represents the whole division, while the decimal represents the quotient with the remainder incorporated as a fractional part.
Divisibility Rules
Divisibility rules are shortcuts to determine if a number is divisible by another without performing long division. While there isn't a specific rule for 5 besides checking for the last digit (ending in 0 or 5), understanding divisibility helps in estimating quotients and remainders.
Prime Numbers and Factors
Understanding the concepts of prime numbers and factors is closely related to division. Prime numbers are numbers only divisible by 1 and themselves. Factors are numbers that divide a given number without leaving a remainder. Analyzing the factors of 12 (1, 2, 3, 4, 6, 12) and 5 (1, 5) gives insight into their divisibility characteristics.
Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
The GCD is the largest number that divides both numbers without a remainder. The LCM is the smallest number that is a multiple of both numbers. Finding the GCD and LCM is crucial in various mathematical problems. For 12 and 5, the GCD is 1 (as they are relatively prime), and the LCM is 60 (12 x 5).
Expanding Our Understanding
The simple problem of 12 divided by 5 with a remainder provides a foundation for understanding more complex mathematical concepts. By mastering the basics of division with remainders, we gain the tools to tackle more challenging problems in arithmetic, algebra, and beyond. The ability to interpret and utilize remainders opens doors to various fields, highlighting its practical importance in real-world applications.
Conclusion
The seemingly trivial problem of 12 divided by 5 reveals the rich tapestry of mathematical concepts underlying even the most basic arithmetic operations. From the simple methods of repeated subtraction and long division to the more advanced concepts of modular arithmetic, fractions, and divisibility rules, we have explored a range of tools and ideas interconnected through the fundamental concept of division with remainders. The applications of this concept extend far beyond the classroom, permeating various aspects of our daily lives and contributing significantly to fields like computer science, cryptography, and engineering. Understanding division with remainders is not just about getting the right answer; it's about grasping the underlying principles that govern the mathematical world. It's a stepping stone to a deeper appreciation of mathematics and its ubiquitous role in our world.
Latest Posts
Latest Posts
-
10 Out Of 21 As A Percentage
May 25, 2025
-
How Many 3 8 Are In 6
May 25, 2025
-
What Is The Greatest Common Factor Of 15 And 35
May 25, 2025
-
How Many Calories Are In 30 Weight Watchers Points
May 25, 2025
-
Income Tax Calculator With Rental Property
May 25, 2025
Related Post
Thank you for visiting our website which covers about 12 Divided By 5 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.